
Versagen im Mathematikunterricht
Eine empirische Untersuchung unter leistungsschwachen Schülern
Diplomarbeit
zur Erlangung des akademischen Grades „Magister der Naturwissenschaften“
an der Formal- und Naturwissenschaftlichen Fakultät der Universität Wien
Feber 1997
| Text herunterladen |
| Original-Datei (Word 95) |
| Betreuer | Günter Hanisch |
| Begutachter | Hans-Christian Reichel |
| Approbiert | am 10. April 1997 |
Entlehnbar in folgenden Bibliotheken:
| Bibliothek | Signatur |
|---|---|
| Österreichische Nationalbibliothek | 1500069-C. Neu Mag |
| Universitätsbibliothek Wien | II-1217171 |
| Fachbereichsbibliothek für Mathematik | 57428 [HoD] |
Inhaltsverzeichnis
- Vorwort: 7
- Vorbemerkungen: 8
- Einleitung: 9
- Theoretische Aspekte: 10
- Umfragedaten: 21
- Auswahl der Befragten: 21
- Die teilnehmenden Institute: 22
- Durchführung der Befragung: 24
- Der Fragebogen: 25
- Leistungsdaten: 25
- Mitarbeit, Lernen: 26
- Ursachen für schlechte Leistungen: 26
- Lernkurs: 26
- Allgemeines: 27
- Angaben zur Person: 27
- Voruntersuchung: 27
- Rücklaufquote: 28
- Korrekturen am Datenmaterial: 28
- Die Auswertung des Fragebogens: 34
- Skalen: 34
- Nominalskalen: 35
- Ordinalskalen: 35
- Intervallskalen: 35
- Rationalskalen: 36
- Skalenniveau der erhobenen Daten: 36
- Statistische Verfahren: 38
- Skalen: 34
- Die Ergebnisse: 58
- Erläuterungen: 58
- Die Variablen im einzelnen: 59
- „1) Was waren Deine Noten in Mathematik im abgelaufenen Schuljahr?“: 59
- Notendurchschnitt aller Schularbeiten und Zeugnisse: 62
- „2) Welche Note würdest Du Dir selbst im Jahreszeugnis geben?“: 67
- Differenz zwischen tatsächlicher und selbst gegebener Note im Jahreszeugnis (in Notenstufen): 68
- „3) Welche Note würdest Du Deinem/r Mathematiklehrer/in geben?“: 72
- „4) Wie oft hast Du schon eine Klasse wiederholt?“: 77
- „5) Wie oft davon warst Du auch in Mathematik negativ?“: 78
- „6) In wie vielen Fächern hast Du eine Wiederholungsprüfung („Nachzipf“)?“: 79
- „7) Darfst Du in jedem Fall aufsteigen (mit „Klausel“)?“: 81
- „8) Wie viele Schüler/innen in Deiner Klasse haben eine Wiederholungsprüfung in Mathematik (Dich eingerechnet)?“: 82
- „9) Wie viele Schüler/innen gehen in Deine Klasse (Dich eingerechnet)?“: 82
- Anteil der Schüler mit Wiederholungsprüfung in Mathematik an der Klassenschülerzahl: 84
- „10) Wie hast Du im Mathematikunterricht aufgepaßt?“: 85
- „11) Wie oft habt Ihr in Mathematik eine Hausübung bekommen?“: 86
- „12) Wie oft hast Du die Hausübung (selbst!) gemacht?“: 87
- „13) Wenn Du die Hausübung nicht (selbst) gemacht hast, warum nicht?“: 89
- „14) Was hältst Du davon, wenn nicht alle Schüler/innen die selbe Hausübung bekommen, sondern eine an ihr Können angepaßte?“: 95
- „15) Wann hast Du im abgelaufenen Schuljahr Mathematik gelernt?“: 96
- „16) Welche Ursachen machst Du für Deine schlechten Leistungen in Mathematik verantwortlich?“: 101
- „17) Besuchst Du diesen Lernkurs freiwillig?“: 114
- „18) Wer oder was hat Dich dazu beeinflußt, diesen Lernkurs zu besuchen?“: 116
- „19) Warum besuchst Du diesen Lernkurs?“: 120
- „20) Was interessiert Dich an Mathematik?“: 125
- „21) Hältst Du den Mathematikunterricht (so wie er bei Dir in der Schule stattfindet) für sinnvoll?“: 127
- „22) Hältst Du Mathematik grundsätzlich als Unterrichtsfach für sinnvoll?“: 129
- „23) Würdest Du es für sinnvoll halten, wenn sich Dein Lehrer mit Dir und Deinen Eltern bereits zu Beginn des zweiten Semesters zusammensetzt, um gemeinsam zu überlegen, wie man ein drohendes „Nicht genügend“ verhindern könnte?“: 130
- „24) Alter“: 132
- „24) Klasse“: 132
- „24) Geschlecht“: 133
- „25) Schule“: 133
- Zusammenfassung: 135
- Anhang 1: Fragebogen: 138
- Anhang 2: Programme: 141
- Abkürzungsverzeichnis: 143
- Literaturverzeichnis: 144
- Fußnoten
Vorwort
Zu Beginn möchte ich all jenen danken, die mich bei dieser Arbeit unterstützt haben:
- meiner Freundin Michaela für die unermüdliche Unterstützung beim elektronischen Erfassen der Fragebögen, sowie für einige wertvolle Hinweise,
- Herrn Univ.-Doz. Mag. Dr. Günter Hanisch für die wirklich ausgezeichnete und entgegenkommende Betreuung,
- meiner Mutter, die mich während des ganzen Studiums unterstützt hat,
- und nicht zuletzt natürlich all jenen Schülern, die den Fragebogen ausgefüllt haben, sowie den Verantwortlichen in den Lerninstituten, die mir die Befragung ermöglichten.
Vorbemerkungen
Im Sinne einer besseren Lesbarkeit und Übersichtlichkeit habe ich auf Formulierungen wie „Schülerinnen und Schüler“, „SchülerInnen“, „Schüler/innen“, „der/die Schüler/in“, „er/sie“, etc. (außer im Fragebogen) verzichtet. Selbstverständlich schließe ich mit der Bezeichnung „Schüler“ sowohl weibliche als auch männliche ein.
Ich bin mir dessen bewußt, daß die Schulnachricht am Ende des ersten Semesters kein Zeugnis ist, benütze diese Bezeichnung einfachheitshalber aber dennoch.
Ich verwende die Kurzzitierweise im laufenden Text (vgl. Theisen, 1992, S. 138): Nach dem Zitat folgt in Klammern der Name des Autors, nach einem Beistrich das Erscheinungsjahr des Werkes, und nach einem weiten Beistrich die Seite der betreffenden Textstelle. Im Fall, daß sich die Textstelle über mehrere Seiten erstreckt, habe ich auf ein angeschlossenes „f“ für „folgende“ verzichtet. Alle bibliographischen Daten des zitierten Werkes sind im Literaturverzeichnis ersichtlich. Bei mehreren Werken desselben Autors in einem Jahr habe ich diese mit Kleinbuchstaben numeriert, also z. B. „Weiss, 1989 a“ und „Weiss, 1989 b“.
Die Namen von Personen stehen einheitlich in Kapitälchen.
Das Literaturverzeichnis enthält ausschließlich in der Arbeit zitierte
oder erwähnte Werke.
Einleitung
Die vorliegende Arbeit befaßt sich mit dem Phänomen des Versagens im Mathematikunterricht. Ihr zugrunde liegt eine empirische Untersuchung mittels Fragebogen unter leistungsschwachen Schülern.
Wie weitverbreitet das untersuchte Problem ist, zeigt die Tatsache, daß im Schuljahr 1994/95 an Wiener AHS die meisten „Nicht genügend“ im Jahreszeugnis im Fach Mathematik gegeben wurden (vgl. Buchacher, 1995, S. 64). Und für den Bereich der BMHS stellte Schwendenwein nach einer Untersuchung fest: „Sowohl in der HTL als auch in Technikerschulen1 ist Mathematik als Versagergegenstand Nummer eins zu bezeichnen.“ (Schwendenwein, 1982, S. 228).
Ziel der Arbeit ist es, das Versagen ganz bewußt aus der Sicht der Schüler zu beleuchten. Dadurch soll jedoch nicht impliziert werden, daß die Schuld am Versagen stets alleine bei den Schülern liegt. Kozmut meint beispielsweise, „daß heute ‘Schulversagen’ noch immer mehrheitlich als ein Versagen der Kinder in der Schule verstanden wird. […] Nur wenige Leute interpretieren das Wort ‘Schulversagen’ als das Versagen der Institution Schule […]. Die Schule selbst produziere ‘Versager’ durch veraltete Lehrpläne und antiquierten Lehrstoff, schlecht ausgebildete und unmotivierte Lehrer mit falschen oder nicht mehr zeitgemäßen Unterrichtsmethoden.“ (Kozmut, 1988, S. 2).
1 Theoretische Aspekte
1.1 Problematik der Leistungsbeurteilung
In der Testtheorie werden an ein Meßinstrument drei klassische Qualitätsanforderungen gestellt (vgl. Ziegenspeck, 1973, S. 170; Ingenkamp, 1977, S. 18; Ullrich & Wöbcke, 1981, S. 20; sehr ausführlich Langfeldt, 1984, S. 68; Ingenkamp, 1989, S. 22; Rieder, 1990, S. 24; sehr ausführlich Sacher, 1991, S. 48; Clauß & Ebner, 1992, S. 34; Clauß, Finze & Partzsch, 1994, S. 12; sehr ausführlich Ingenkamp, 1995, S. 34):
- Objektivität
- Validität
- Reliabilität
Eine Messung heißt objektiv, wenn das Ergebnis unabhängig von der Person des Versuchsleiters ist, d. h., wenn beim selben Sachverhalt verschiedene Personen immer zum selben Ergebnis gelangen.
Als valid oder gültig wird eine Messung dann bezeichnet, wenn sie tatsächlich das mißt, was sie zu messen vorgibt, d. h., wenn keine „fremden“ Faktoren die Messung beeinflussen.
Das Kriterium der Reliabilität oder Zuverläßlichkeit schließlich ist genau dann erfüllt, wenn die Messung genau ist. In der Praxis wird das meist dadurch festgestellt, indem beobachtet wird, ob die Messung bei wiederholter Durchführung stets das selbe Ergebnis liefert.
Zahlreiche Untersuchungen belegen, daß das bei uns übliche System der Ziffernnoten keine dieser drei Anforderungen in zufriedenstellendem Maße erfüllt (vgl. Dumke, 1973, S. 51; Ingenkamp, 1977, S. 19; die Reduktion von individueller mathematischer Leistungsfähigkeit zu einer Gesamtnote behandelt Ossimitz, 1985, S. 199; einen guten Überblick über die gesamte Problematik der Leistungsbeurteilung bietet Weiss, 1989 a; Ingenkamp, 1995, S. 106). Die Auswahl an Literatur ist dabei so groß, daß ich mich auf einige Untersuchungen zur Mathematik beschränken möchte, zumal dadurch die Annahme, daß gerade Mathematik jenes Fach sei, in dem eine objektive Beurteilung am besten möglich ist, eindrucksvoll widerlegt wird.
So stellten Starch & Elliot schon 1913 fest, „wie absurd die Vorstellung
ist, eine Mathematikarbeit sei präziser zu bewerten als eine Sprache oder
irgendeine andere Art von Prüfungsarbeiten.“ (Starch & Elliot,
1989, S. 85). Sie ließen die selbe schriftliche Geometriearbeit von 128
amerikanischen Mathematiklehrern mit dem jeweils schulüblichen Punktesystem
bewerten. Die kritische Marke zum Bestehen einer Arbeit betrug je nach Schule
70, 75 oder 80 Punkte; die größtmögliche Punktezahl war ebenfalls
unterschiedlich.
Die größte Streuung war in der Gruppe der Schulen mit kritischem
Wert 70 zu verzeichnen: Die 43 Bewertungen reichten von 25 bis 89 Punkte!
49 Lehrer beurteilten jede Frage einzeln und verwendeten dazu eine Skala von
0 bis 12½. Bei einer der zehn Fragen der Arbeit streuten die Bewertungen
dabei sogar von 0 bis 12½ (vgl. Starch & Elliot, 1989, S. 84).
In Österreich wurde die Problematik von Weiss 1964 untersucht: Er legte je eine Rechenarbeit der 4. und eine der 5. Schulstufe 153 bzw. 119 Lehrern zur Beurteilung vor. Die 153 Benotungen der Arbeit aus der 4. Schulstufe reichten von 1 bis 5, jene der 5. Schulstufe von 2 bis 5 (vgl. Weiss, 1989 b, S. 104).
Außerdem wurde der Einfluß von Vorurteilen auf die Benotung nachgewiesen:
Ein Teil der Lehrer erhielt die Information, die Arbeit der 4. Schulstufe würde
von „einem mathematisch begabten Buben mit einer Neigung zu originellen
Lösungen“ stammen, während es bei jener der 5. Schulstufe hieß,
sie stamme von „einem durchschnittlich begabten Buben.“ und: „Die
Original-Arbeit fiel durch unsaubere Form und schlampige Schrift auf.“
(Weiss, 1989 b, S. 108). Dem anderen Teil der Lehrer wurden die selben Informationen
vertauscht geboten.
Das Ausmaß der Abweichung war dabei in der 4. Schulstufe „sehr signifikant,
in der 5. Schulstufe nicht signifikant.“ (Weiss, 1989 b, S. 116).
1973 ließ Weiss erneut 24 Volksschullehrer eine Mathematikarbeit der 4. Schulstufe und 10 Hauptschullehrer eine der 5. Schulstufe beurteilen. In beiden Gruppen reichten die Noten ebenfalls von 1 bis 5 (vgl. Weiss, 1989 a, S. 115).
Hanisch legte insgesamt 42 Lehrern zwei verschiedene Schülerarbeiten der selben Schularbeit (5. Schulstufe) zur Benotung vor (19 Lehrer bekamen die eine Arbeit („Gruppe A“), 23 die andere („Gruppe B“)). In Gruppe A streuten die Noten von 2 bis 5, in Gruppe B von 3 bis 5 (vgl. Hanisch, 1990, S. 169).
Eine Untersuchung über die Reliabilität von Mathematiknoten veröffentlichte Dicker 1973. Er ließ 24 deutsche Lehrer die selbe Schülerarbeit einer 5. Schulstufe im Abstand von 3 Monaten zwei mal benoten. Durch die Versuchsanordnung war die Wahrscheinlichkeit, daß sich ein Lehrer bei der zweiten Beurteilung noch an die erste erinnern konnte, gering. Die Auswertung der Unterschiede ergab eine signifikante Abweichung, die jedoch in keinem Fall größer als eine Notenstufe war (vgl. Dicker, 1989, S. 173).
1.2 Bezugsnormen der Leistungsbeurteilung
Um die Leistung eines Schülers einschätzen zu können, ist es notwendig, sie in Bezug zu anderen Leistungen zu setzen. Nur so kann beurteilt werden, ob die Leistung gut oder schlecht war.
Die Information, daß ein Schüler bei einem Test 90 von 100 Punkten erreicht hat, ist zuwenig, um aussagen zu können, ob er gut oder schlecht abgeschnitten hat. Vielleicht war der Test so schwer, daß niemand außer ihm über 50 Punkte erreicht hat. Vielleicht war er aber auch so leicht, daß alle anderen 100 Punkte erzielt haben. Vielleicht hat der selbe Schüler ein Monat davor bei einem vergleichbaren Test nur 70 Punkte bekommen, vielleicht aber auch 100.
In der pädagogischen Literatur werden drei verschiedene Bezugsnormen für die Leistungsbeurteilung unterschieden (vgl. Heckhausen, 1980, S. 575; sehr ausführlich Rheinberg, 1980, S. 16; speziell auf das Schulversagen abgestimmt Schwarzer, 1980, S. 11; Ullrich & Wöbcke, 1981, S. 35; Rheinberg, 1987, S. 88; eine testtheoretische Kritik bietet Klauer, 1987, S. 184; Weiss, 1989 a, S. 54; ausführlich Aberschek, 1990, S. 64; ausführlich Rieder, 1990, S. 27; sehr ausführlich Sacher, 1991, S. 76 und S. 111; Ingenkamp, 1995, S. 44):
- die individuelle Bezugsnorm
- die soziale Bezugsnorm
- die sachliche Bezugsnorm
Bei der individuellen Bezugsnorm wird die aktuelle Leistung des Schülers im Vergleich zu seinen bisher erbrachten Leistungen gesehen. So kann zwar ausgesagt werden, ob er sich verbessert oder verschlechtert hat, ob er über oder unter seinem Leistungsniveau geblieben ist, jedoch nicht, ob er eine an sich gute Leistung erbracht hat.
Im Fall der sozialen Bezugsnorm beurteilt man die aktuelle Leistung eines Schülers im Vergleich zu den aktuellen Leistungen anderer Schüler (z. B. einer Klasse oder Leistungsgruppe). Dadurch erkennt man, ob er diesbezüglich zu den Leistungsstärkeren oder Leistungsschwächeren in der Gruppe zählt. Für unsere Thematik bedeutsam ist die Tatsache, daß es bei dieser Bezugsnorm stets Schüler mit schlechten Noten gibt, und zwar weitgehend unabhängig davon, ob diese Schüler an sich schlechte Leistungen erbringen (zur sozialen Bezugsnorm vgl. Weidig, 1961, S. 24; Birkel, 1984, S. 237; eine ausführliche Kritik bietet Sacher, 1984, S. 15).
Die sachliche Bezugsnorm schließlich orientiert sich rein an der Aufgabe: Eine Leistung wird als gut beurteilt, wenn sie über den gesetzten Anforderungen liegt, und als schlecht, wenn sie unter ihnen zurückbleibt. Diese Methode scheint zwar auf den ersten Blick die bestgeeignete zu sein, da sie als einzige etwas über die Leistung an sich aussagt, im Schulbereich jedoch zeigt sich ihre Schwäche insofern, als die gestellten Anforderungen je nach Lehrer variieren und man nicht aussagen kann, inwieweit sie realistisch sind.
Auf die Tatsache, daß die bei Lehrern weitverbreitete soziale Bezugsnorm gerade die für schlechte Schülern ungeeignetste ist, soll hier nicht näher eingegangen werden. Der interessierte Leser sei auf andere Autoren verwiesen: Heckhausen, 1980, S. 580; sehr ausführlich Rheinberg, 1980; Garnitschnig, 1990, S. 177; ausführlich Persy, 1990, S. 156.
1.3 Die Definition von Versagen
Eine Definition von Versagen ist schwierig, weil es sich um einen Gegenstand handelt, „über den bis heute keine begriffliche Klarheit herrscht. […] Verschiedene Autoren sprechen von Lernstörungen, Leistungsversagen, Lernschwäche, Lernbeeinträchtigung, erwartungswidrigen Minderleistungen, Schwierigkeiten im Lernprozeß oder Auffälligkeiten im Lern- und Leistungsbereich. Es handelt sich um Beschreibungsbegriffe, die sich inhaltlich stark überlappen und auf zum Teil unterschiedliche theoretische Zugänge hinweisen.“ (Schwarzer, 1980, S. 9).
In der Literatur habe ich keine allgemein anerkannte Definition von Versagen gefunden. Melber kommt im Rahmen ihrer Untersuchung „leistungsschwacher Schüler in den Leibesübungen“ ebenfalls zu dem Schluß, daß es keine Übereinstimmung darüber gibt, „wann ein Schüler als leistungsschwach zu bezeichnen ist“ (Melber, 1988, S. 11).
In Anlehnung an die drei Bezugsnormen der Leistungsbeurteilung lassen sich auch drei Arten der Definition von Versagen unterscheiden:
- „absolute Definitionen“ in Anlehnung an die sachliche
Bezugsnorm:
Einteilung durch eine gewisse (möglichst eindeutig feststellbare) Eigenschaft (z. B. Zeugnisnoten). - „relative Definitionen“ in Anlehnung an die soziale
Bezugsnorm:
Klassifikation eines gewissen Anteils an Schülern als Versager (z. B. das jeweils schlechteste Viertel der Klasse). - „individuelle Definitionen“ in Anlehnung an die
individuelle Bezugsnorm:
Festsetzung des Versagens aufgrund des Vergleichs mit bisher erbrachten Leistungen.
1.3.1 Absolute Definitionen
Bei absoluten Definitionen besteht die Gefahr, daß durch ungeschickte Wahl der entscheidenden Eigenschaft für das Versagen weitaus mehr Schüler als Versager klassifiziert werden, als beabsichtigt war und auch sinnvoll ist.
Diesem Fehler erlag z. B. Scharf in ihrer Untersuchung über Schulversagen. Sie unterteilte die Probanden danach in G („ohne Lernschwierigkeiten“, gut) und S („mit Lernschwierigkeiten“, schlecht), ob sie in irgendeinem Fach ein „Genügend“ oder „Nicht genügend“ erwarteten (vgl. Scharf, 1988, S. 41). Wie nicht anders zu erwarten, wurden dabei über 80% der Befragten als S klassifiziert (vgl. Scharf, 1988, S. 53). Eine solche Einteilung, wonach die große Mehrheit der Schüler als schlecht gilt, erscheint mir nicht sinnvoll.
Geschickter geht Pritz-Garger vor, wenn sie in ihrer zweistufigen Untersuchung die befragten Schüler in drei Versuchsgruppen spaltet: Im ersten Teil der Erhebung (im Mai) wurden die Schüler danach eingeteilt, ob sie „einen Bescheid erhielten, der besagte, daß ihnen ein oder mehrere Nicht genügend im Jahreszeugnis drohten2 (Pritz-Garger, 1984, S. 54). Diejenigen, die eine solche Verständigung erhalten hatten, wurden im zweiten Teil (im September) weiter unterteilt, und zwar hinsichtlich dessen, ob sie zum Aufsteigen berechtigt waren oder nicht3 (vgl. Pritz-Garger, 1984, S. 55). Dabei wurde die Hälfte der Schüler (51%) als „gut“ (d. h. ohne Gefährdung im Mai), ein Drittel (35%) als „Gefährdete“ (d. h. mit Gefährdung im Mai, allerdings im September zum Aufsteigen berechtigt) und 14% als „Schulversager“ (nicht zum Aufsteigen berechtigt) ausgewiesen (Pritz-Garger, 1984, S. 56). Als Versager wird somit weniger als ein Siebentel der Schüler bezeichnet, als potentielle Versager allerdings schon die Hälfte.
Die meiner Ansicht nach für unsere Thematik sinnvollste und gleichzeitig wohl am weitesten verbreitete Definition stammt von Krapp. Er sieht Schulerfolg und Schulversagen als qualitative Kategorien, die zum Ausdruck bringen, „daß die individuell erbrachten Leistungen eine von der Schule festgelegte Mindestanforderungsnorm über- oder unterschreiten.“ (Krapp, 1984, S. 47). Da mit „Mindestanforderung“ wohl nur die Anforderungen zum Aufsteigen in die nächste Klasse gemeint sein können, sind genau jene Schulversager, die nicht zum Aufsteigen berechtigt sind.
Ganz ähnlich schreibt Tiedemann: „Zum Schulleistungsversagen kommt es immer dann, wenn diese kumulativen Schulleistungen4 die von der Schule geforderten ständig ansteigenden Anforderungen – die Anforderungsschwelle – unterschreiten“ (Tiedemann, 1978, S. 17).
Ebenso definiert Seidl im Rahmen seiner Untersuchung im Schuljahr 1965/66: „Als Versager wurden jene Schüler bestimmt, die wegen unzureichenden Leistungen in ihrer Schule die Berechtigung zum Aufstieg in die nächst höhere Klasse nicht erhielten. Nach dieser Definition sind auch jene Schüler, die während des Jahres das Gymnasium mit einem ungenügenden Erfolg verlassen haben, zu den Versagern zu rechnen.“ (Seidl, 1967, S. 4).
Auch das „Pädagogische Lexikon“ erklärt Schulversagen als „Mißerfolg, gemessen an den lehrplanmäßigen Leistungszielen der Schule, also in altersstufen- und schulgattungsspezifischen Formen. Die Schule kennt Schulversagen in allen Schweregraden bei unterschiedlichen Erscheinungsformen (vom verdeckten, latenten bis zum offenen Schulversagen des Sitzenbleibers). […]“ (Engelmayer, 1970, S. 959).
Wittoch schließlich weist darauf hin, daß je nach Zusammenhang bzw. beteiligten Personen verschiedene Sachverhalte als Schulversagen bezeichnet werden können. Schließlich räumt sie aber ein: „Eine Klassenwiederholung ist für den betroffenen Schüler, seine Eltern und Geschwister, die Klassenkameraden, Freunde und Freundinnen und auch für den Lehrer schon ein sehr deutliches Zeichen, daß hier Versagen vorliegt.“ (Wittoch, 1976, S. 13)
1.3.2 Relative Definitionen
Bei relativen Definitionen wird Versagen in Bezug zu einer gewissen Schülergruppe (z. B. der Klasse) definiert. Dabei besteht die Gefahr, durch ungeschickte Wahl des Vergleichskriteriums annähernd konstante und zu hohe Anteile an Versagern auszuweisen; oder, wie Rieder formuliert: „Die soziale Bezugsnorm produziert somit immer eine bestimmte Anzahl von ‘Versagern’“ (Rieder, 1990, S. 28).
Schwendenwein allerdings scheint bei seiner Auseinandersetzung mit verschiedenen Definitionen überhaupt Probleme mit dem Begriff „Durchschnitt“ zu haben, wenn er meint: „Wenn beispielsweise unterdurchschnittliche Noten schlechte Schüler kennzeichnen, dann scheinen höhere Schulen hauptsächlich von solchen besucht zu werden, was eine im Schuljahr 1975/76 von Karas durchgeführte Erhebung von Jahresnoten bei rund 10.000 Schülern alles AHS des Bundeslandes Salzburg eindeutig nachweist. […] Demnach dominieren in Englisch, Latein, zweiter lebender Fremdsprache oder Griechisch sowie in Mathematik, vor allem in der Oberstufe unterdurchschnittliche Zensuren, was den voreiligen Schluß zuließe, daß ein Großteil der AHS-Besucher aus unbegabten bzw. ungeeigneten oder sogenannten schlechten Schülern bestünde“ (Schwendenwein, 1982, S. 32). Der Leser möge selbst beurteilen, wie es möglich ist, daß die Mehrzahl der Schüler unter dem Durchschnitt liegt. Der einzige voreilige Schluß, der sich mir aufdrängt, ist, daß Schwendenwein als Durchschnittsnote die Note „3“ ansieht (weil sie in der Mitte der Notenskala liegt), was aber an der statistischen Definition des Durchschnitts weit vorbeigeht.
Das eingangs erwähnte Problem eines konstant zu hohen Anteils an Versagern entsteht bei der aus dem Bereich der Leibesübungen stammenden Definition Grotefents: „Unter dem Terminus ‘leistungsschwach’ fassen wir in Übereinstimmung mit der Fachliteratur die Kinder und Jugendlichen zusammen, die […] in ihrer körperlichen Leistungsfähigkeit unter dem Durchschnitt ihrer Alterskameraden liegen“ (Grotefent, 1969, S. 80). Demnach wäre stets rund die Hälfte aller Schüler leistungsschwach.
Hoschek behebt diesen Fehler durch Einfügung des Wortes „deutlich“ (ebenfalls für Leibesübungen): „Als leistungsschwache Schüler werden jene Schüler bezeichnet, die […] deutlich unter der Norm ihrer Klassenkameraden liegen.“ (Hoschek, 1983, S. 228).
Höhn und Wandl ermittelten die schlechten Schüler in ihren Untersuchungen (Höhn: 1958 bis 1960, Wandl: 1982 bis 1984) dadurch, daß sie den Lehrer einer Klasse die Schüler in vier (Höhn) bzw. drei (Wandl) Leistungsgruppen einteilen lassen (Höhn, 1980, S. 124 und Wandl, 1987, S. 61). Diese Vorgangsweise erscheint mir allerdings nur dann sinnvoll, wenn (wie bei den betreffenden Untersuchungen) die Lage des schlechten Schülers im Klassenverband untersucht werden soll. Höhn berichtet, daß die Verteilung auf die vier Gruppen „im ganzen“ „ziemlich gleichmäßig“ erfolgte: Der schlechtesten Gruppe wurde knapp ein Fünftel der Schüler zugerechnet (Höhn, 1980, S. 124).
Die Vorgangsweise von Höhn und Wandl hat zwar den Vorteil, daß der Anteil der Versager nicht zu hoch angenommen wird (da wohl kein Lehrer den Großteil seiner Klasse im schlechtesten Drittel bzw. Viertel ansiedeln wird), andererseits aber den Nachteil, daß auch dort Versager ausgewiesen werden, wo eigentlich gar keine sind (da kein Lehrer niemanden in die unterste Gruppe einordnen wird).
1.3.3 Individuelle Definitionen
Bei diesem, in der Literatur nur selten vertretenen, Ansatz wird Versagen als deutliches Zurückbleiben hinter den persönlichen Leistungsmöglichkeiten definiert. Diese Vorgangsweise ist jedoch schwierig, da aus den bisherigen Leistungen des Schülers auf sein Leistungspotential geschlossen werden muß. Versagt hat der Schüler dann, wenn er bei einer in diesem Sinne „angemessenen“ Aufgabe deutlich unter seinem üblichen Leistungsniveau bleibt. Daher ist diese Art der Definition für die Praxis nur beschränkt brauchbar, und es soll hier nicht näher darauf eingegangen werden.
1.3.4 Resümee
Die zuvor erörterte Frage nach der Definition von Versagen beantwortet jeder Leiter einer diesbezüglichen Untersuchung indirekt durch die Auswahl der Versuchspersonen. Ich habe mich entschlossen, Schüler, die in den Sommerferien einen Mathematikkurs besuchten, zu befragen. Damit folge ich im wesentlichen der absoluten Definition des Versagens, indem ich mich auf Schüler konzentriere, die Gefahr laufen, die Berechtigung zum Aufsteigen in die nächste Schulstufe nicht zu erlangen.
2 Umfragedaten
2.1 Auswahl der Befragten
Befragt wurden Schüler, die in den Sommerferien 1996 in Wien einen Mathematikkurs bei einem professionellen Lerninstitut (meist ein Vorbereitungskurs auf die Wiederholungsprüfung) besucht haben. Die Befragung dauerte von Montag, dem 22. Juli 1996, bis Anfang September 1996.
Durch diese Auswahl ist die Gruppe der Befragten einerseits sehr klar abgegrenzt und andererseits sind die interessierenden Schüler auch leicht zu erreichen. Da die Zahl der Schüler, die einen Lernkurs besuchen, nicht übermäßig groß ist, ist sogar eine Totalerhebung möglich.
Es stellt sich natürlich die Frage, inwieweit die gewählte Probandengruppe mit der Gruppe der Mathematikversager übereinstimmt. Eine völlige Übereinstimmung ist selbstverständlich nicht gegeben, da es viele Gründe gibt, warum ein leistungsschwacher Schüler keinen Kurs besucht, z. B.:
- er muß die Klasse in jedem Fall wiederholen,
- er lernt alleine oder mit Nachhilfe,
- er kann sich die Kursgebühr nicht leisten,
- er bricht die Schule ab.
Eine Befragung aller leistungsschwachen Schüler in Mathematik (z. B. jener, die ein „Nicht genügend“ im Jahreszeugnis haben), wäre zwar aussagekräftiger, vom Standpunkt des notwendigen Aufwandes allerdings unvertretbar: Es müßten entweder die interessierenden Schüler gezielt befragt werden, was nur mit einigem Aufwand möglich wäre, oder sie müßten aus einer Auswahl aller Schüler (nicht nur leistungsschwacher) gefiltert werden; dabei wäre allerdings eine für statistische Berechnungen hinreichend große Anzahl von leistungsschwachen Schülern erst bei Befragung von weit über 1000 Schülern zu erwarten. Im Vergleich zu der von mir gewählten Vorgangsweise sind beide Alternativen also unökonomisch.
Um mit überschaubarem Aufwand eine solche Anzahl von Schülern erreichen zu können, ist man außerdem auf die Mithilfe von Lehrern angewiesen. Dabei würde ich allerdings mit gröberen Verzerrungen rechnen, da die Gefahr besteht, daß sich genau jene Lehrer weigern würden, an der Untersuchung teilzunehmen, bei denen besonders viele Schüler schlechte Leistungen erbracht haben.
Es haben zwar auch nicht alle Lerninstitute der Befragung zugestimmt, jedoch dürften dadurch keine systematischen Verzerrungen aufgetreten sein, da nicht zu erwarten ist, daß bestimmte Schülertypen ausgerechnet diese Institute bevorzugen.
2.2 Die teilnehmenden Institute
Die angesprochenen Lerninstitute erwiesen sich größtenteils als sehr entgegenkommend. Die meisten sagten sofort ihre Unterstützung zu.
Von den 31 Wiener Lerninstituten5 haben folgende 15 an der Umfrage teilgenommen (gereiht nach Anzahl der retournierten Fragebögen):
| Institut | Fragebögen |
|---|---|
| Volkshochschule Margareten (Polycolleg) | 68 |
| AFM Argentinierstraße | 46 |
| IFL-Lernhilfe Dr. Rampitsch | 43 |
| Volkshochschule Favoriten | 35 |
| AFM Mariahilfer Straße | 33 |
| Jugendzentrum Donaustadt | 30 |
| SMI-Lernhilfe durch Professoren | 30 |
| Lernen 8 | 23 |
| Volkshochschule Urania | 23 |
| Volkshochschule Wien Nord West | 21 |
| Volkshochschule Hietzing | 15 |
| Volkshochschule Liesing | 14 |
| Lernhilfe Studio | 12 |
| Volkshochschule Simmering | 7 |
| Bildungsbüro Walch | 4 |
| Summe | 404 |
An dieser Stelle möchte ich mich noch einmal sehr herzlich für die freundliche Unterstützung bei allen Verantwortlichen und Schülern bedanken!
Folgende 3 Institute weigerten sich, an der Untersuchung teilzunehmen:
LHI
Mandl-Institut Wien
Zwei davon gaben keine Begründung an, eines berief sich auf den Datenschutz. Dieser Begriff wird in letzter Zeit leider oft auch dann strapaziert, wenn er – so wie in diesem Zusammenhang – vollkommen fehl am Platze ist: Die Befragung war nämlich einerseits anonym und andererseits freiwillig, wodurch jeder selbst entscheiden konnte, ob er z. B. Angaben zu seiner Person machen will oder nicht.
Folgende 5 Institute haben im Untersuchungszeitraum keine Mathematikkurse angeboten:
Volkshochschule Brigittenau
Volkshochschule Floridsdorf
Volkshochschule Donaustadt
Berlitz-Sprachschule
Mit folgenden 8 Instituten wurde vereinbart, daß sich eine Befragung aufgrund der geringen Schülerzahl nicht rentiert oder aus organisatorischen Gründen nicht möglich ist:
Multilingua
ÖGB - Fachgruppe Privatlehrer
Pi-Quadrat
Schülerzentrum
Volkshochschule Penzing
Volkshochschule Wien West
Wiener Lehrerklub
2.3 Durchführung der Befragung
Die überwiegende Mehrzahl der Institute war bestrebt, eine Störung des Unterrichts durch die Befragung zu vermeiden. Die Fragebögen wurden daher meist von den Kursleitern an die Schüler verteilt, von diesen zu Hause ausgefüllt, an die Kursleiter zurückgegeben und von mir schließlich gesammelt abgeholt.
2.4 Der Fragebogen
Der Fragebogen6 besteht im wesentlichen aus 6 Teilen:
- Leistungsdaten (Fragen 1 bis 9)
- Mitarbeit, Lernen (Fragen 10 bis 15)
- Ursachen für schlechte Leistungen (Frage 16)
- Lernkurs (Fragen 17 bis 19)
- Allgemeines (Fragen 20 bis 23)
- Angaben zur Person (Fragen 24 bis 25)
2.4.1 Leistungsdaten
Die einleitenden Fragen zur Leistung (mit Ausnahme der Fragen 2 und 3 nach der Selbstbeurteilung und der Beurteilung des Mathematiklehrers) heben sich insofern von den folgenden ab, als sie die einzigen sind, die objektiv zu beantworten sind.
Dieser Fragenkomplex dient dazu, ein Bild über die schulische Leistungssituation des Schülers zu erhalten. Die Entwicklung der Fragen gestaltete sich schwierig, da es sich um einen relativ komplexen Sachverhalt handelt, der aber in wenigen Fragen erfaßt werden muß, um die Schüler bei der Beantwortung nicht zu langweilen.
Mein Ziel war es herauszufinden, ob der Schüler heuer zum ersten Mal in Mathematik „schlecht“ ist, ob er noch in anderen Fächern „hängt“ und wenn ja, in wie vielen und wie lange schon.
2.4.2 Mitarbeit, Lernen
Hier sollte herausgefunden werden, wie der Schüler sein Lernverhalten im abgelaufenen Schuljahr einschätzt. Die schwer zu beantwortende Frage, ob Aufpassen und Hausübungen Machen bereits als Lernen zu werten ist, habe ich der Einschätzung des Schülers überlassen. Durch die getrennten Fragen nach Aufpassen, Hausübung und Lernen (in dieser Reihenfolge) wurde jedenfalls die Möglichkeit zur Trennung gegeben.
Bei diesen Fragen kommt die subjektive Sicht des Schülers natürlich stark zum Tragen, was aber beabsichtigt war (siehe Einleitung, Seite 9).
2.4.3 Ursachen für schlechte Leistungen
In der meiner Ansicht nach wichtigsten Frage geht es um die Ursachen, die der befragte Schüler subjektiv für seine schlechten Leistungen in Mathematik verantwortlich macht. Diese persönliche Einschätzung kann natürlich noch stärker als bei den vorigen Fragen von den wahren Ursachen abweichen, allerdings ist die subjektive Ursachenzuschreibung für eine Verbesserung der Leistungen des Schülers sicherlich von zentraler Bedeutung.
2.4.4 Lernkurs
Die Fragen nach dem Lernkurs zielen hauptsächlich darauf ab, ob der Schüler den Kurs aus freien Stücken besucht bzw. von wem er beeinflußt wurde.
2.4.5 Allgemeines
Hier soll die Einstellung des Schülers zur Mathematik im allgemeinen und im Unterschied dazu zum Mathematikunterricht in seiner Schule im besonderen festgestellt werden.
Die Frage nach der Sinnhaftigkeit eines sogenannten „Frühwarnsystems“ (Frage 23) habe ich gestellt, weil es im (mittlerweile beschlossenen) „Schulreformpaket“ (SchUG-Novelle vom 30. Dezember 1996) enthalten ist. Dabei ist es mir sinnvoll erschienen, abseits von politischen Strategien die persönliche Meinung der Betroffenen zu hören, ob sie sich mit ihrem Lehrer und mit ihren Eltern ein solches Gespräch vorstellen können.
2.4.6 Angaben zur Person
Die abschließenden Angaben zur Person und zur besuchten Schule dienen dazu, Vergleichsgruppen unter den Schülern bilden zu können.
2.5 Voruntersuchung
Um die Verständlichkeit des Fragebogens zu überprüfen, habe ich vor Beginn der Hauptuntersuchung eine Voruntersuchung an einigen Jugendlichen durchgeführt. Dabei wurden 20 mir bis dahin unbekannte Personen im Alter von 16 bis 18 Jahren befragt, von denen 13 den Fragebogen ausfüllten, während ihn sich 7 durchlasen.
2.6 Rücklaufquote
Die Angabe einer Rücklaufquote ist aufgrund der Vorgangsweise nicht möglich. Da es mir unzumutbar erschien, von den Instituten zu verlangen, die eingesammelten Fragebögen zu zählen bzw. den Verbleib der Fragebögen zu überwachen, kann nicht rekonstruiert werden, aus welchem der folgenden Gründe in fast allen Fällen weniger Fragebögen retourniert als hingebracht wurden:
- Der Fragebogen wurde von einem Schüler zwar angenommen aber nicht ausgefüllt.
- Der Fragebogen wurde von einem Schüler zwar ausgefüllt aber nicht abgegeben.
- Die übriggebliebenen leeren Fragebögen wurden von den Kursleitern oder vom Institut weggeworfen.
Von den 404 retournierten Fragebögen waren drei unbrauchbar: Eine Schülerin besucht die Waldorfschule, daher sind die Angaben mit Schülern aus Regelschulen nicht vergleichbar; eine Schülerin ist Externistin, besucht also überhaupt keine Schule und nur ein einziger Fragebogen war offensichtlich mangelhaft ausgefüllt. In die Auswertung wurden also 401 Fragebögen aufgenommen.
2.7 Korrekturen am Datenmaterial
Vor Auswertung der Daten habe ich sie nach verschiedenen Kriterien auf ihre Plausibilität hin geprüft. Das war notwendig, um beispielsweise widersprüchliche Angaben, die das Ergebnis verfälschen würden, zu löschen. Selbstverständlich bin ich dabei sehr behutsam vorgegangen und habe die Antworten im Zweifelsfall auf „Missing“7 gesetzt. Dadurch wird der „falsche“ Wert zwar gestrichen, die Antwortverteilung jedoch nicht verfälscht.
Folgende Änderungen habe ich vorgenommen:
- Bei mehreren angekreuzten Werten oder Von-Bis-Angaben wurde der Mittelwert gewertet. Im ersten Fall kann angenommen werden, daß der Zwischenwert gemeint war; bei von Von-Bis-Werten (z. B. bei der Frage nach der Anzahl der Schüler in der Klasse) beruht diese Ersetzung auf der Hoffnung, daß sich die Abweichungen nach oben und unten ungefähr die Waage halten. Die Alternative wäre gewesen, den Wert auf „Missing“ zu setzen, was mir aber als Datenverlust erschienen ist.
- Bei den fünf freien Variablen („welcher?“, „wann?“, „was?“, „was/wer?“, „welcher?“) habe ich redundante Aussagen auf „Missing“ gesetzt; das sind solche, die bereits im Fragenblock darüber als Antwortalternative angeboten waren. Die Gewichtungsvariable („anderer Grund“, „wann anders“, „etwas anderes“, „etwas anderes / jemand anderer“, „anderer Grund“) wurde dabei ebenfalls auf „Missing“ gesetzt.
- Die verbleibenden Angaben habe ich behutsam zu einheitlichen Antworten zusammengefaßt (z. B. „faul“, „zu faul“, „war zu faul“, „Faulheit“ einheitlich auf „faul“). Dadurch gehen in Einzelfällen zwar Bedeutungsnuancen verloren, im Sinne einer besseren Übersicht ist dies aber unvermeidlich.
- Wenn jemand bei Frage 4 („Wie oft hast Du schon eine Klasse wiederholt?“) „0 mal“ angekreuzt hat, bei Frage 5 („Wie oft davon warst Du auch in Mathematik negativ?“) allerdings „1 mal“ oder „2 mal“, dann habe ich die Frage 5 ebenfalls auf „0 mal“ gesetzt. Das war bei 54 Fragebögen der Fall. Der Grund dafür dürfte darin liegen, daß der Schüler das Wort „davon“ in Frage 5 überlesen hat und daher angegeben hat, wie oft er überhaupt in Mathematik „negativ“ war.
- Wenn jemand bei Frage 4 „1 mal“ angegeben hat, jedoch bei Frage 5 „2 mal“, dann habe ich die Frage 5 ebenfalls auf „1 mal“ gesetzt, in der Hoffnung, daß dies die richtige Antwort ist. Das war bei 11 Fragebögen der Fall. Es wäre nämlich auch möglich, daß der Schüler zwar schon einmal eine Klasse wiederholt hat, dabei aber nicht in Mathematik „negativ“ war, sondern in zwei anderen Jahren, in denen er allerdings aufsteigen durfte.
- Auf einem Fragebogen wurde bei Frage 8 („Wie viele Schüler/innen in Deiner Klasse haben eine Wiederholungsprüfung (Dich eingerechnet)?“) mit „3“ geantwortet, jedoch zusätzlich angemerkt: „10 Pers. fallen durch“. In diesem Fall habe ich die Antwort auf „13“ gesetzt.
- Wenn jemand bei Frage 12 („Wie oft hast Du die Hausübung
(selbst!) gemacht?“) „1“ (für „immer“)
angekreuzt hat, bei Frage 13 („Wenn Du die Hausübung nicht (selbst)
gemacht hast, warum nicht?“) jedoch trotzdem diverse Gründe angegeben
hat, habe ich die Frage 13 auf „Missing“ gesetzt, wenn sie ursprünglich
einheitlich beantwortet worden war (also z. B. nur mit „5“).
Das war bei 7 Fragebögen der Fall. Durch die Änderung wollte ich
eine Verzerrung der Frage 13 vermeiden.
War die Frage 13 jedoch ursprünglich uneinheitlich beantwortet worden, so habe ich die Daten nicht verändert in der Annahme, daß dadurch die Gründe aufgezeigt wurden, falls der Schüler die Hausübung doch einmal nicht gemacht hat. - 22 Personen haben angegeben, daß sie die Note „5“
im Jahreszeugnis, jedoch keine Wiederholungsprüfung haben. Eine Schülerin
vermerkte neben Frage 6 („In wie vielen Fächern hast Du eine
Wiederholungsprüfung („Nachzipf“)?“) „Bin durchgefallen“.
In diesem Fall habe ich die Antwort auf „Missing“ gesetzt.
17 Schüler gaben bei Frage 19 („Warum besuchst Du diesen Lernkurs?“) bei der Alternative „wegen der Wiederholungsprüfung“ den Wert 1 oder 2 an bzw. vermerkten bei andern Fragen einen Hinweis auf die Wiederholungsprüfung. Dadurch habe ich angenommen, daß sie die Frage 6 falsch verstanden haben, und habe die Antwort ebenfalls auf „Missing“ gesetzt. - Nach dieser Korrektur blieben noch acht Schüler, die
angegeben haben, daß sie keine Wiederholungsprüfung haben, und
dennoch nicht in jedem Fall aufsteigen dürfen (Frage 7). Davon haben
drei ebenfalls bei Frage 19 die Alternative „wegen der Wiederholungsprüfung“
mit 1 oder 2 bewertet. Daher habe ich die Anzahl der Wiederholungsprüfungen
(Frage 6) auf „Missing“ gesetzt.
Weitere drei haben eine „positive“ Jahreszeugnisnote und bei Frage 19 bei der Alternative „wegen der Wiederholungsprüfung“ gar nichts oder den Wert 5 angegeben. Dadurch habe ich angenommen, daß sie die Frage 7 falsch verstanden haben, und habe diese auf „Missing“ gesetzt. - Jetzt verblieben noch drei Schüler ohne Wiederholungsprüfung, die trotzdem bei Frage 19 die Alternative „wegen der Wiederholungsprüfung“ mit 1 oder 2 bewertet haben. Auch bei diesen habe ich angenommen, daß sie die Frage 6 falsch verstanden haben, und habe die Antwort auf „Missing“ gesetzt.
- Eine Schülerin hat bei Frage 13 („Wenn Du die Hausübung nicht (selbst) gemacht hast, warum nicht?“) bei jeder Antwortalternative „1“ für „Trifft voll zu“ angegeben, und bei „anderer Grund“ – „welcher?“ „Vergessen“ geschrieben. Da das den anderen Alternativen widerspricht, habe ich alle Antworten der Frage 13 auf „Missing“ gesetzt.
- Wenn jemand auf die Frage 20 („Was interessiert Dich
an Mathematik?“) bei jeder Antwortalternative „1“ (für
„Sehr“) angekreuzt hat, so habe ich alle Alternativen auf „Missing“
gesetzt, da die Antworten „nichts, ich will nur durchkommen“
und „die Regeln zur Beispiellösung“ bzw. „die dahinterliegenden
Ideen“ nicht alle voll zutreffen können. Das war bei 5 Fragebögen
der Fall.
Weitere 30 Personen haben ebenfalls alle Antwortalternativen einheitlich beantwortet, allerdings mit „3“, „4“ bzw. „5“. In diesen Fällen habe ich nichts geändert. - Bei näherer Betrachtung der Daten hat sich gezeigt,
daß mehrere Schüler bei manchen Fragenblöcken (Fragen 13,
15, 16, 18, 19) nur jeweils einige Alternativen bewertet haben und alle
anderen unbeantwortet ließen. Da in diesen Fällen angenommen
werden kann, daß außer den bewerteten Alternativen für
den Schüler keine anderen relevant sind, habe ich die nicht beantworteten
Alternativen auf „5“ (für „Trifft gar nicht zu“,
„Gar nicht gelernt“, „Gar nicht“, „Gar nicht
beeinflußt“, „Gar nicht“) gesetzt, wenn alle folgenden
Bedingungen erfüllt waren:
- Es waren nicht alle Alternativen unbeantwortet.
Sonst muß nämlich angenommen werden, daß sich der Schüler entweder nicht hinreichend mit der Frage auseinandergesetzt hat oder daß er sich für keine Antwortmöglichkeit entscheiden konnte. - Es waren mindestens drei Alternativen unbeantwortet.
Bei weniger als drei unbewerteten Antwortmöglichkeiten ist eher anzunehmen, daß der Schüler diesbezüglich keine Antwort geben wollte bzw. konnte; es kann jedoch nicht darauf geschlossen werden, daß diese Punkte irrelevant für ihn waren. - Es war keine Alternative mit „5“ beantwortet.
Hat ein Schüler nämlich andere Alternativen mit „5“ bewertet, so kann nicht angenommen werden, daß er nur die für ihn zutreffenden Punkte angekreuzt hat, weshalb eine Änderung der unbewerteten Antwortmöglichkeiten nicht zulässig ist.
Bei Frage 13 wurden in 41 Fällen Änderungen vorgenommen bei Frage 15 in 75 Fällen, bei Frage 16 in 39 Fällen, bei Frage 18 in 63 Fällen und bei Frage 19 in 56 Fällen. - Es waren nicht alle Alternativen unbeantwortet.
3 Die Auswertung des Fragebogens
3.1 Skalen
In der Statistik werden empirische Tatsachen (sogenannte Eigenschaften) durch Messungen erhoben. Die Meßergebnisse werden meist in Zahlen dargestellt. Eine solche Abbildung, die jeder Eigenschaft eine Bezeichnung (meist eine Zahl) zuordnet, heißt Skala. Da sinnvollerweise die Beziehungen zwischen den Eigenschaften durch die Abbildung erhalten bleiben sollen, ist eine Skala meist ein Homomorphismus (vgl. Langfeldt, 1984, S. 65; Fischer, 1991, S. 69; Sacher, 1991, S. 42 und S. 48; Ingenkamp, 1995, S. 27; Fahrmeir & Hamerle, 1996, S. 4)
Je nach Art der Eigenschaft ergeben sich qualitativ verschiedene Skalen. (vgl. Ziegenspeck, 1973, S. 66; Ziegenspeck, 1978, S. 624; Ullrich & Wöbcke, 1981, S. 18; Langfeldt, 1984, S. 66; Weiss, 1989 a, S. 61; Rieder, 1990, S. 22; ausführlich Diehl & Kohr, 1991, S. 8; Fischer, 1991, S. 73; Sacher, 1991, S. 44; Clauß & Ebner, 1992, S. 25; Hartung, Elpelt & Klösener 1993, S. 16; Clauß, Finze & Partzsch, 1994, S. 51; Heiler & Michels, 1994, S. 22; Bühl & Zöfel, 1995, S. 91; Ingenkamp, 1995, S. 29; Backhaus, Erichson, Plinke & Weiber, 1996, S. XV; Vogel, 1996, S. 5):
3.1.1 Nominalskalen
Bei einer Nominalskala unterscheiden sich die einzelnen Werte ausschließlich qualitativ. Zwischen den verschiedenen Eigenschaften gibt es keine Rangordnung. Arithmetische Operationen aller Art sind daher nicht zulässig.
Beispiele:
Geschlecht: männlich – weiblich
Haarfarbe: rot – blond – braun – schwarz
Mittagessen: Schnitzel – Salatplatte – Gulasch
3.1.2 Ordinalskalen
Im Fall einer Ordinalskala sind die Meßwerte geordnet, jedoch bestehen unterschiedliche Abstände zwischen den Werten. Eine Darstellung durch Zahlen ist zwar sinnvoll, allerdings muß beachtet werden, daß der Abstand vom Wert „1“ zum Wert „2“ anders sein kann als vom Wert „3“ zum Wert „4“. Additionen und komplexere arithmetische Operationen sind daher nicht zulässig.
Beispiele:
Häufigkeitsangaben in Fragebögen: immer – meistens – manchmal
– selten – nie
Alphabetische Reihenfolge: Maier – Mayr – Meier – Meyer
Rechengeschwindigkeit von Computerprozessoren: 286 – 386 – 486 –
Pentium
3.1.3 Intervallskalen
Intervallskalenniveau ist dann gegeben, wenn die Meßwerte geordnet sind und zwei aufeinanderfolgende Werte stets den selben Abstand haben. Eine Darstellung durch Zahlen ist daher höchst sinnvoll, allerdings sind nur Additionen und Subtraktionen zulässig, jedoch keine Multiplikationen und Divisionen.
Beispiele:
Temperatur: 0°C – 1°C – 2°C
Jahreszahlen: 1988 – 1992 – 1996 (aufgrund der Schalttage in Vierjahressprüngen)
Uhrzeit: 1 Uhr – 2 Uhr – 3 Uhr
3.1.4 Rationalskalen
Rationalskalen stellen das höchste Skalenniveau dar. Dabei haben die Meßwerte nicht nur konstante Abstände, sondern es existiert auch ein empirischer Nullpunkt, d. h., wenn einem Objekt der Skalenwert „0“ zugeordnet wird, besitzt das Objekt nichts von der gemessenen Eigenschaft. Additionen, Subtraktionen, Multiplikationen und Divisionen sind zulässig.
Beispiele:
Gewicht: 0 kg – 1 kg – 2 kg
Länge: 0 m – 1 m – 2 m
Zeitdauer: 0 min – 1 min – 2 min
3.1.5 Skalenniveau der erhobenen Daten
Vor der statistischen Auswertung jedes Datenmaterials ist es notwendig, das Skalenniveau der Daten festzustellen, da davon abhängig ist, welche statistischen Verfahren zulässig sind. Diese Frage ist keine statistische, sondern muß inhaltlich entschieden werden.
Auf einen Blick erkenntlich ist das Skalenniveau bei folgenden Fragen:
Die Fragen 7, 25 und „Geschlecht“ (bei Frage 24) sowie die 5 offenen Fragen „welcher?“, „wann?“, „was?“, „was/wer?“ und „welcher?“ (in den Fragen 13, 15, 16, 18 und 19) sind nominalskaliert.
Die Frage „Klasse“ (bei Frage 24) ist intervallskaliert.
Die Fragen 4, 5, 6, 8, 9 und „Alter“ (bei Frage 24) sind rationalskaliert.
Die Fragen 1 bis 3 sind mit Schulnoten zu beantworten; es gilt also, deren
Skalenniveau festzustellen.
In der Literatur herrscht weitgehende Einigkeit darüber, daß Schulnoten
nicht, wie auf den ersten Blick vielleicht vermutet, intervallskaliert, sondern
lediglich ordinalskaliert sind, da die Abstände zwischen den einzelnen
Noten nicht konstant sind, da beispielsweise der leistungsmäßige
Unterschied zwischen den Noten „4“ und „5“ größer
sein kann, als zwischen „1“ und „2“ (vgl. Ziegenspeck, 1973, S. 67; Ziegenspeck, 1978, S. 625; Langfeldt, 1984, S. 67; Sacher, 1984,
S. 10; Weiss, 1989 a, S. 62; Rieder, 1990, S. 23; Sacher, 1991, S. 45; Clauß & Ebner, 1992, S. 26; Reichel, Hanisch & Müller, 1992, S. 13; Hartung,
Elpelt & Klösener, 1993, S. 16; Heiler & Michels, 1994, S. 22;
Ingenkamp, 1995, S. 31).
Die Fragen 10 bis 23 sind (mit Ausnahme der 5 offenen Fragen) auf einer 5stufigen numerischen Ratingskala zu beantworten, wobei „1“ stets völlige Zustimmung (z. B. „Trifft voll zu“, „Sehr“) und „5“ völlige Ablehnung (z. B. „Trifft gar nicht zu“, „Gar nicht“) ausdrücken. Es kann angenommen werden, daß die Schüler die 5stufige Unterteilung als äquidistant aufgefaßt haben und die Daten daher Intervallskalenniveau besitzen (vgl. Fischer, 1991, S. 76; Backhaus, Erichson, Plinke & Weiber, 1996, S. XVI).
Da Schulnoten nur Ordinalskalenniveau erreichen, sind genaugenommen sämtliche Rechenverfahren, die auf Summierung basieren (wie z. B. Mittelwertbildung), unzulässig. Dies wird einerseits dann deutlich, wenn man sich vor Augen hält, daß die Ziffernnoten nur bequemere Schreibweisen der „verbalen“ Noten „Sehr gut“ bis „Nicht genügend“ darstellen, und andererseits, weil Ordinalskalen invariant gegenüber streng monotonen Transformationen sind, d. h. man könnte genauso gut die Zahlen „1“, „2“, „3“, „10“, „370“ als Noten nehmen, wodurch Mittelwertschwankungen von 5 bis 200 durchaus vorstellbar wären.
In der Schulpraxis setzt man sich jedoch über diese Tatsache weitgehend hinweg, meist ohne sich – wie ich zu behaupten wage – der Problematik bewußt zu sein (eine ausführliche Kritik bietet Sacher, 1984, S. 9). Reichel, Hanisch & Müller weisen jedoch darauf hin, daß Notendurchschnitte „doch eine gewisse Aussagekraft“ haben, eben weil unsere Schulnoten äquidistant von 1 bis 5 sind (Reichel, Hanisch & Müller, 1992, S. 31). Aus diesem Grund habe auch ich die Berechnung von Notendurchschnitten vorgenommen (ebenso Clauß & Ebner, 1992, S. 26).
3.2 Statistische Verfahren
In den folgenden Kapiteln möchte ich die bei der Auswertung des Fragebogens verwendeten statistischen Verfahren vorstellen. Die Ergebnisse sowie die Prüfung der Voraussetzungen sind im folgenden Abschnitt bei den einzelnen Variablen dargestellt.
Detailliert gehe ich nur auf den Rangkorrelationskoeffizienten von Kendall ein, da es sich mit Ausnahme dieses durchwegs um weitverbreitete Standardverfahren handelt. Für den interessierten Leser gebe ich am Ende jedes Verfahrens weiterführende Literaturhinweise.
Die Auswertung des Fragebogens erfolgte mit der Statistiksoftware SPSS für Windows 6.0.1. Da die Berechnung des multiplen Rangkorrelationskoeffizienten in diesem Programm jedoch nicht möglich ist, habe ich dieses Verfahren selbst in Derive 3.00 programmiert (siehe Anhang 2, Seite 141). Als Ausgangsbasis dienten dabei die von SPSS berechneten bivariaten Rangkorrelationskoeffizienten.
3.2.1 Der Rangkorrelationskoeffizient von Kendall
Der am weitesten verbreitete Maßkorrelationskoeffizient r von Pearson setzt intervallskalierte Daten voraus, weshalb er für Berechnungen im Zusammenhang mit Schulnoten unzulässig ist.
Für Daten auf Ordinalskalenniveau bieten sich der Rangkorrelationskoeffizient von Spearman und jener von Kendall an. Der Spearmansche ist zwar bekannter, jedoch ist ihm der von Kendall vorzuziehen, weil der Spearmansche eigentlich nur eine Abwandlung des Maßkorrelationskoeffizienten darstellt, bei dem die Rangplätze als Meßwerte eingesetzt werden; außerdem ist die Behandlung von identischen Meßwerten nicht hinreichend geklärt, was gerade im vorliegenden Fall stark ins Gewicht fällt, da die Antwortmöglichkeit bei den meisten Fragen nur von 1 bis 5 reicht. (vgl. Röhr, Lohse & Ludwig, 1983, S. 162).
3.2.1.1 Die Berechnung des Rangkorrelationskoeffizienten
In der Literatur ist der Koeffizient von Kendall unterschiedlich und teilweise widersprüchlich definiert. Ich folge Röhr, Lohse & Ludwig, 1983, da mir diese Definition (auch speziell für den vorliegenden Fall) am geeignetsten erscheint.
Wie in der Literatur üblich, bezeichne ich den Koeffizienten von Kendall im folgenden als „τ“.
Die Meßwerte x'i und y'i der Variablen X und Y werden so in Rangplätze xi und yi transformiert, daß dem kleinsten Meßwert der Rang 1 zugewiesen wird, dem zweitkleinsten der Rang 2 usw. Die Methode sei an folgender Tabelle erläutert:
| i (Nummer der Versuchsperson) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| x'i (Meßwert in X) | 105 | 98 | 117 | 124 | 80 | 132 | 103 | 91 |
| xi (Rangplatz in X) | 5 | 3 | 6 | 7 | 1 | 8 | 4 | 2 |
| y'i (Meßwert in Y) | 17 | 24 | 9 | 13 | 5 | 25 | 16 | 20 |
| yi (Rangplatz in Y) | 5 | 7 | 2 | 3 | 1 | 8 | 4 | 6 |
Sind mehrere Meßwerte identisch, so müßte ihnen der selbe Rangplatz zugeordnet werden. In diesem Fall spricht man von einer Rangbindung.
Es werden alle Paare von Versuchspersonen gebildet. Bei n Versuchspersonen
sind das ![]() Paare.
Paare.
Nun werden die Ränge in X und in Y jedes Paares miteinander verglichen.
Ein Paar ![]() heißt:
heißt:
| Proversion oder konkordant, falls | xi <= xj und yi < yj
oder xi >= xj und yi > yj. |
| Inversion oder diskordant, falls | xi <= xj und yi > yj
oder xi >= xj und yi < yj. |
Sei nun P:= Anzahl der Proversionen,
I:= Anzahl der Inversionen und
A:= Anzahl aller Paare = ![]() .
.
Die sogenannte Kendall-Summe ist dann definiert als S:= P–I.
S ist bereits ein Maß für den Zusammenhang der beiden Variablen
X und Y, allerdings kann S (bei hinreichend großen Stichproben mit vielen
Proversionen) beliebig große Werte annehmen, weshalb es als Korrelationskoeffizient
ungeeignet ist. Aus diesem Grund wird τ folgendermaßen definiert:
![]() .
.
Smax ist dabei der Maximalwert von S; also jener Wert, der angenommen
wird, wenn I=0 ist.
Die Bestimmung von S erfolgt stets durch Auszählung der Proversionen und Inversionen; für Smax spielen jedoch eventuelle Rangbindungen eine entscheidende Rolle, auf die im folgenden eingegangen wird.
3.2.1.2 1. Fall: Keine Rangbindungen
In diesem Fall ist Smax=A, da jedes Paar entweder eine Proversion
oder eine Inversion ist.
τ läßt
sich daher darstellen als ![]() .
.
Für praktische Zwecke ist folgende weitere Vereinfachung hilfreich, da
bei dieser nur die Zählung der Inversionen, nicht jedoch der Proversionen,
nötig ist.
Für A wird ![]() eingesetzt und P=A–I wird substituiert:
eingesetzt und P=A–I wird substituiert:
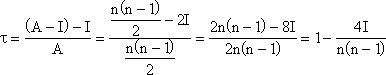 .
.
Zur Abzählung der Inversionen empfiehlt es sich, die Versuchspersonen nach xi (Rangplätze in X) zu ordnen. Die X- und Y-Rangplätze einer Versuchsperson werden dann wie im folgenden Beispiel untereinander geschrieben:
| i | 5 | 1 | 9 | 6 | 10 | 3 | 4 | 7 | 2 | 8 |
|---|---|---|---|---|---|---|---|---|---|---|
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| yi | 2 | 6 | 1 | 4 | 8 | 7 | 5 | 3 | 9 | 10 |
Bemerkung: Die erste Zeile gibt die Nummer der Versuchsperson an. Diese ist zufällig, da nicht angenommen werden kann, daß ausgerechnet die erste Versuchsperson den kleinsten X-Meßwert liefert, die zweite den zweitkleinsten, usw.
Nun betrachtet man y5=2 und zählt alle folgenden yi, die kleiner sind, ab. Hier ist das eines, nämlich y9=1. Dann rückt man weiter zu y1=6 und zählt alle folgenden (also rechts davon stehenden) yi, die kleiner sind, dazu. Hier sind das vier, nämlich y9=1, y6=4, y4=5 und y7=3; insgesamt haben wir also bis jetzt fünf Inversionen gezählt. So fährt man fort und erhält in diesem Beispiel 12 Inversionen (zu den bisherigen fünf noch eine bei y6=4, drei bei y10=8, zwei bei y3=7 und eine bei y4=5).
Mittels obiger Formel können wir τ
nun schnell berechnen:
![]() .
.
3.2.1.3 2. Fall: Rangbindungen in Y
Im Fall von mehreren identischen Meßwerten ist jedem davon als Rangplatz der Mittelwert der in Frage kommenden Rangplätze zuzuordnen, wie es folgende Tabelle zeigt (zur Verdeutlichung habe ich auch die y'j (Meßwerte in Y) angegeben):
| i | 5 | 9 | 1 | 3 | 10 | 4 | 6 | 8 | 2 | 7 |
|---|---|---|---|---|---|---|---|---|---|---|
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y'i | 23 | 27 | 23 | 35 | 27 | 43 | 35 | 44 | 35 | 35 |
| yi | 1,5 | 3,5 | 1,5 | 6,5 | 3,5 | 9 | 6,5 | 10 | 6,5 | 6,5 |
Hier ist y'5 = y'1 = 23; das sind die beiden niedrigsten Werte, folglich wären ihnen die Rangplätze 1 und 2 zuzuordnen. Es ist also der Mittelwert von 1 und 2 zu bilden und beiden als Rangplatz zu vergeben (y5 = y1 = 1,5). Analog erhalten die identischen Werte y'9 = y'10 = 27 den gemittelten Rangplatz 3,5 und y'3 = y'6 = y'2 = y'7 = 35 den Rang 6,5.
Da nun außer Proversionen und Inversionen auch sogenannte Ambiversionen (Paare mit gleichen Y-Rangplätzen) auftreten, genügt es nicht mehr, zur Bestimmung von S nur die Inversionen auszuzählen.
Ebenso ist Smax nicht mehr gleich der Anzahl aller Paare, sondern
muß um K:= Anzahl der Ambiversionen verringert werden.
Diese muß allerdings nicht abgezählt werden, sondern kann über
folgende Formel berechnet werden:
![]() .
.
Dabei ist b2:= Anzahl der Paarbindungen,
b3:= Anzahl der Dreierbindungen, …
bk:= Anzahl der k-Bindungen.
Der Koeffizient bi von gibt die Anzahl der Paare an, die aus i Personen
gebildet werden können. Analog zu A ist er gleich ![]() .
.
Für die sogenannte maximale bindungskorrigierte Kendall-Summe S*max
gilt somit: ![]() .
.
Und für das bindungskorrigierte τ*:
![]() .
.
Wir rechnen das obige Beispiel fertig:
Zur Bestimmung der Proversionen beginnen wir bei y5 = 1,5. Es bestehen
acht Proversionen, und zwar mit jedem folgenden yi, außer mit
y1 = 1,5, da dies eine Ambiversion ist. Insgesamt erhalten wir 30
Proversionen (zu den acht noch sechs bei y9 = 3,5, sieben bei y1
= 1,5, zwei bei y3 = 6,5, fünf bei y10 = 3,5 und
je eine bei y4 = 9 und y6 = 6,5). Analog zählen wir
7 Inversionen (je eine bei y9 = 3,5 und y3 = 6,5, drei
bei y4 = 9 und zwei bei y8 = 10). Also ist S=30–7=23.
Zur Berechnung von K betrachten wir die Ambiversionen: Es gibt zwei Paar- und eine Viererbindung; es ist also b2 = 2 und b4 = 1. Somit ist K=2+6·1=8. Dieses Ergebnis können wir auch leicht durch Abzählen der Ambiversionen in der Tabelle überprüfen.
Weiters ist somit ![]() und schließlich
und schließlich ![]() .
.
3.2.1.4 3. Fall: Rangbindungen in X und Y
In diesem Fall liegen sowohl in X als auch in Y identische Meßwerte vor, weshalb in beiden Variablen Rangbindungen auftreten:
| i | 7 | 1 | 9 | 5 | 10 | 8 | 6 | 4 | 3 | 2 |
|---|---|---|---|---|---|---|---|---|---|---|
| x'i | 12 | 15 | 15 | 15 | 18 | 21 | 22 | 27 | 27 | 30 |
| xi | 1 | 3 | 3 | 3 | 5 | 6 | 7 | 8,5 | 8,5 | 10 |
| y'i | 92 | 89 | 93 | 93 | 93 | 95 | 95 | 95 | 96 | 96 |
| yi | 2 | 1 | 4 | 4 | 4 | 7 | 7 | 7 | 9,5 | 9,5 |
Hier erweist sich auch die bisher einfache Abzählung der Inversionen und Proversionen als problematisch, da die Reihenfolge der Versuchspersonen (und damit der Y-Ränge) aufgrund der Bindungen in X nicht mehr eindeutig ist. In der Tabelle ist dies beispielsweise bei y1 = 1 und y9 = 4 der Fall: Die zugehörigen X-Ränge sind x1 = x9 = 3 und können daher nicht der Größe nach geordnet werden. Die Entscheidung, welcher der beiden X-Ränge als erster angeschrieben wird, ist aber insofern wesentlich, als aufgrund der verschiedenen Y-Ränge im einen Fall eine Proversion, im anderen jedoch eine Inversion vorliegt.
Gelöst wird dieses Problem dadurch, daß die zu Bindungen in X gehörigen
Y-Ränge einmal vom kleinsten zum größten, und dann vom größten
zum kleinsten angeordnet werden. Dann wird für beide Varianten S berechnet
(zur Unterscheidung S*+ und S*–
genannt) und die doppelt-bindungskorrigierte Kendall-Summe S**
als Mittelwert der beiden gebildet:
![]()
Für obige Tabelle ergeben sich:
37 Proversionen (je acht bei y7 = 2 und y1 = 1, je fünf
bei y9 = 4, y5 = 4 und y10 = 4, je zwei bei
y8 = 7, y6 = 7 und y4 = 7) und 1 Inversion
(bei y7 = 2). Die erste Kendall-Summe lautet daher: S*+
= 37–1=36.
Nun werden die Y-Ränge innerhalb der Bindungen in X vertauscht:
| i | 7 | 1 | 9 | 5 | 10 | 8 | 6 | 4 | 3 | 2 |
|---|---|---|---|---|---|---|---|---|---|---|
| xi | 1 | 3 | 3 | 3 | 5 | 6 | 7 | 8,5 | 8,5 | 10 |
| yi | 2 | 4 | 4 | 1 | 4 | 7 | 7 | 9,5 | 7 | 9,5 |
Dadurch ergeben sich 34 Proversionen (acht bei y7 = 2, je fünf
bei y1 = 4 und y9 = 4, sechs bei y5 = 1, fünf
bei y10 = 4, je zwei bei y8 = 7 und y6 = 7
und eine bei y3 = 7) und 4 Inversionen (je eine bei y7
= 2, y1 = 4, y9 = 4 und y4 = 9,5). Die zweite
Kendall-Summe ist daher: S*– = 34–4=30.
Somit ist klar: ![]() .
.
Die nächste Schwierigkeit ergibt sich bei der Berechnung der maximalen
doppelt-bindungskorrigierten Kendall-Summe S**max. Anders
als bei S*max müssen hier nämlich nicht nur
Y-, sondern auch X-Bindungen berücksichtigt werden. Dazu definieren wir:
L:= Anzahl der Bindungen in X.
S**max lautet dann:
![]() .
.
Zurück zu unserem Beispiel:
In Y liegen eine Paarbindung und zwei Dreierbindungen vor; Für K ergibt
sich daher: K=1+3·2=7.
Analog berechnet sich L aufgrund je einer Paar- und einer Dreierbindung in X:
L=1+3·1=4.
Daher ist: ![]() .
.
Der doppelt-bindungskorrigierte Koeffizient τ** schließlich lautet allgemein:
![]() .
.
In unserem Beispiel: ![]() .
.
Literatur: Röhr, Lohse & Ludwig, 1983, S. 162; Diehl & Kohr, 1991, S. 289; Hartung & Elpelt, 1992, S. 199; Hartung, Elpelt & Klösener, 1993, S. 559; Heiler & Michels, 1994, S. 267; Janssen & Laatz, 1994, S. 233; Vogel, 1996, S. 61.
3.2.2 Der partielle Rangkorrelationskoeffizient
Der partielle Korrelationskoeffizient ![]() gibt die Korrelation zwischen X1 und X2, bereinigt um
den Einfluß von X3 an. Das ist dann von Bedeutung, wenn untersucht
werden soll, ob zwischen X1 und X2 nur eine sogenannte
Scheinkorrelation besteht, die durch das gemeinsame Auftreten mit X3
verursacht wird. So besteht beispielsweise zweifellos eine hohe Korrelation
zwischen Nasenlänge und Intelligenzalter. Diese ist jedoch dadurch verursacht,
daß die Nasenlänge mit dem Alter korreliert und dieses wiederum naturgemäß
mit dem Intelligenzalter. Die partielle Korrelation zwischen der Nasenlänge
und dem Intelligenzalter bereinigt um den Einfluß des Alters wäre
also gering.
gibt die Korrelation zwischen X1 und X2, bereinigt um
den Einfluß von X3 an. Das ist dann von Bedeutung, wenn untersucht
werden soll, ob zwischen X1 und X2 nur eine sogenannte
Scheinkorrelation besteht, die durch das gemeinsame Auftreten mit X3
verursacht wird. So besteht beispielsweise zweifellos eine hohe Korrelation
zwischen Nasenlänge und Intelligenzalter. Diese ist jedoch dadurch verursacht,
daß die Nasenlänge mit dem Alter korreliert und dieses wiederum naturgemäß
mit dem Intelligenzalter. Die partielle Korrelation zwischen der Nasenlänge
und dem Intelligenzalter bereinigt um den Einfluß des Alters wäre
also gering.
Die Berechnung des partiellen und des multiplen Rangkorrelationskoeffizienten erfolgt vollkommen analog zum partiellen bzw. multiplen Maßkorrelationskoeffizienten, weshalb auf die Herleitung der Formeln hier nicht näher eingegangen werden soll.
Wie in der Literatur üblich, schreibe ich für den partiellen Rangkorrelationskoeffizienten
zwischen den Variablen X1X2·X3 statt
![]() kurz τ12·3.
kurz τ12·3.
Die Berechnung erfolgt analog zum partiellen Maßkorrelationskoeffizienten
r12·3 über die Formel:
![]()
Ebenfalls analog zum partiellen Maßkorrelationskoeffizienten r12·34…n
ergibt sich der allgemeine partielle Rangkorrelationskoeffizient:
![]()
Literatur: Röhr, Lohse & Ludwig, 1983, S. 176 und S. 193; Hartung & Elpelt, 1992, S. 181.
3.2.3 Der multiple Rangkorrelationskoeffizient
Der multiple Korrelationskoeffizient ![]() gibt die „gemeinsame“ Korrelation von X1 mit X2
und X3 an. Sie drückt aus, inwieweit X1 mit X2
und X3 gemeinsam auftritt. So kann beispielsweise die Korrelation
zwischen Intelligenzalter und Alter wahrscheinlich erhöht werden, wenn
zusätzlich die Rechenleistung in die (multiple) Korrelation aufgenommen
wird, da die Rechenleistung wahrscheinlich einen gewissen Teil der Varianz des
Intelligenzalters erklären kann, der vom Alter unerklärt bleibt.
gibt die „gemeinsame“ Korrelation von X1 mit X2
und X3 an. Sie drückt aus, inwieweit X1 mit X2
und X3 gemeinsam auftritt. So kann beispielsweise die Korrelation
zwischen Intelligenzalter und Alter wahrscheinlich erhöht werden, wenn
zusätzlich die Rechenleistung in die (multiple) Korrelation aufgenommen
wird, da die Rechenleistung wahrscheinlich einen gewissen Teil der Varianz des
Intelligenzalters erklären kann, der vom Alter unerklärt bleibt.
Analog zum multiplen Maßkorrelationskoeffizienten r1·23 definiert Moran den multiplen Rangkorrelationskoeffizienten:
![]() .
.
Und allgemein analog zu r1·23…n :
![]()
Literatur: Röhr, Lohse & Ludwig, 1983, S. 207 und S. 212; Hartung & Elpelt, 1992, S. 167.
3.2.4 Regressionsanalyse
Die Regressionsanalyse prüft, inwieweit eine abhängige Variable durch eine oder mehrere unabhängige Variable beeinflußt wird. Im Fall von mehreren unabhängigen Variablen spricht man von einer multiplen Regressionsanalyse; wenn ein linearer Zusammenhang zwischen der abhängigen und der/den unabhängigen Variablen geprüft werden soll, von einer linearen Regressionsanalyse; diese ist der Normalfall.
Das Verfahren versucht, alle Meßwerte der interessierenden Variablen
durch eine einzige Funktion zu approximieren; im linearen Fall mit nur einer
unabhängigen Variablen ist diese Funktion eine Gerade. Als Funktion wird
jene ausgewählt, bei der die Summe der quadrierten Abstände zu den
Meßwerten minimal ist.
Eine multivariate lineare Regressionsgleichung mit Y als abhängiger und
X1,X2,…Xn als unabhängige Variable hat
die Gestalt:
Y = c1X1+c2X2+…+cnXn+k
.
Dabei heißt ci Regressionskoeffizient der Variablen Xi;
k ist der konstante Regressionskoeffizient. Die Größe eines Regressionskoeffizienten
gibt Aufschluß über die Stärke des Einflusses der zugehörigen
Variablen auf die abhängige Variable; das Vorzeichen des Koeffizienten
gibt die Richtung der Wirkung an.
Die Regressionsfunktion erklärt einen gewissen Teil der Varianz der abhängigen Variablen, indem sie diese auf den Einfluß der unabhängigen Variablen zurückführt. Die Nullhypothese besagt, daß die unabhängigen Variablen keinerlei systematischen Einfluß auf die abhängige Variable haben. Zur Signifikanzprüfung wird das Verhältnis des durch die Regressionsfunktion erklärten Teils der Varianz zur nicht erklärten Varianz betrachtet und berechnet, wie wahrscheinlich das vorliegende Verhältnis ist, wenn die Nullhypothese zutrifft. Liegt diese Wahrscheinlichkeit unter der vorgegebenen Irrtumswahrscheinlichkeit, kann die Nullhypothese verworfen werden.
Eine Regressionsanalyse setzt die Intervallskalierung der Variablen sowie einige weitere Bedingungen voraus, auf die ich im folgenden eingehe:
Wenn zwischen zwei oder mehreren unabhängigen Variablen starke Zusammenhänge bestehen, liegt Kollinearität vor. Dies hat zwar keinen Einfluß auf die Signifikanzprüfung der Regressionsgleichung insgesamt, kann jedoch zu Verzerrungen der einzelnen Regressionskoeffizienten führen, sodaß falsche Aussagen über die Einflußstärke der einzelnen unabhängigen Variablen entstehen können. Zur Überprüfung der Kollinearität dienen drei Indikatoren, auf die ich jedoch nicht näher eingehen möchte, nämlich die Toleranz, der Konditionsindex sowie die den Eigenwerte zugeordneten Varianzanteile.
Die Residuen (das sind die Abweichungen der Meßwerte von der Regressionsfunktion) müssen zufällig verteilt sein. Diese Bedingung wird einerseits durch Vergleich mit der Normalverteilung, andererseits mit dem Durbin & Watson-Koeffizienten geprüft. Letzterer gibt das Ausmaß der Autokorrelation der Residuen an, d. h., inwieweit zwischen den Residuen aufeinanderfolgender Fälle systematische Zusammenhänge bestehen. Der Koeffizient kann Werte von 0 bis 4 annehmen, wobei 2 keinerlei Autokorrelation bedeutet.
Literatur: Röhr, Lohse & Ludwig, 1983, S. 238; Diehl & Kohr, 1991, S. 311; Hartung & Elpelt, 1992, S. 77; Hartung, Elpelt & Klösener, 1993, S. 569; Clauß, Finze & Partzsch, 1994, S. 340; Janssen & Laatz, 1994, S. 359; Brosius & Brosius, 1995, S. 471; Bühl & Zöfel, 1995, S. 307; Backhaus, Erichson, Plinke & Weiber, 1996, S. 1; Fahrmeir, Kaufmann & Kredler, 1996, S. 93.
3.2.5 t-Test
Der t-Test für unabhängige Stichproben untersucht, ob zwischen zwei Gruppen von Versuchspersonen signifikante Unterschiede hinsichtlich des Antwortverhaltens bei einer bestimmten Variablen bestehen. Die Nullhypothese besagt, daß sich die beiden Gruppen nicht unterscheiden. Diese wird getestet, indem berechnet wird, wie wahrscheinlich die vorliegende Differenz zwischen den Mittelwerten ist, wenn die Nullhypothese zutrifft. Die Nullhypothese wird verworfen, wenn diese Wahrscheinlichkeit unter der vorgegebenen Irrtumswahrscheinlichkeit liegt.
Der t-Test setzt voraus, daß die abhängige Variable intervallskaliert und in beiden Gruppen normalverteilt ist.
Literatur: Fischer, 1992, S. 168; Hartung, Elpelt & Klösener, 1993, S. 536; Clauß, Finze & Partzsch, 1994, S. 249; Janssen & Laatz, 1994, S. 293; Brosius & Brosius, 1995, S. 401; Bühl & Zöfel, 1995, S. 252; Güttler, 1996, S. 111.
3.2.6 U-Test
Der U-Test von Mann & Whitney untersucht ebenfalls die Frage, ob sich zwei Gruppen von Versuchspersonen bezüglich einer bestimmten Variablen systematisch unterscheiden. Im Unterschied zum t-Test werden jedoch nicht die Mittelwerte der beiden Gruppen betrachtet, sondern die Rangplätze der Versuchspersonen. Diese werden in eine Rangreihe gebracht und dann werden ähnlich wie beim Rangkorrelationskoeffizienten von Kendall die Inversionen gezählt, d. h., wie oft eine Person aus der ersten Gruppe vor einer aus der zweiten Gruppe in der Rangreihe steht. Die Nullhypothese besagt analog zum t-Test, daß zwischen den Gruppen keine systematischen Unterschiede bestehen. Es wird berechnet, wie wahrscheinlich die ermittelte Anzahl an Inversionen unter Annahme der Nullhypothese ist. Auch hier wird die Nullhypothese verworfen, wenn diese Wahrscheinlichkeit unter der vorgegebenen Irrtumswahrscheinlichkeit liegt.
Der U-Test setzt lediglich Ordinalskalenniveau voraus, hat aber den Nachteil, daß er nicht ganz so effizient arbeitet wie der t-Test, d. h., daß die vorliegenden Abweichungen größer sein müssen, um als signifikant erkannt zu werden.
Literatur: Fischer, 1992, S. 225; Hartung, Elpelt & Klösener, 1993, S. 513; Clauß, Finze & Partzsch, 1994, S. 221; Janssen & Laatz, 1994, S. 425; Brosius & Brosius, 1995, S. 520; Bühl & Zöfel, 1995, S. 268.
3.2.7 Varianzanalyse
Ähnlich wie der t-Test untersucht die Varianzanalyse Unterschiede zwischen verschiedenen Gruppen, allerdings können hier mehrere abhängige Variable bei mehr als zwei Gruppen (mehrere unabhängige Variable) gleichzeitig untersucht werden. Die unabhängigen Variablen, die zur Unterteilung in Vergleichsgruppen herangezogen werden, heißen Faktoren, ihre verschiedenen Ausprägungen Faktorstufen. Nach diesen Faktorstufen werden die Versuchspersonen in sogenannte Zellen zusammengefaßt; bei beispielsweise zwei unabhängigen Variablen, wovon die eine zwei, die andere drei Ausprägungen (Faktorstufen) besitzt, entstehen sechs Zellen.
Die Bezeichnungen für verschiedene Arten der Varianzanalyse sind in der Literatur leider uneinheitlich und daher etwas verwirrend. Mir erscheint folgende Notation am zweckmäßigsten: Eine Varianzanalyse mit nur einer abhängigen Variablen heißt univariat, eine mit mehreren abhängigen Variablen multivariat. Je nach Anzahl der unabhängigen Variablen (Faktoren) wird unterschieden zwischen einfaktoriell und mehrfaktoriell.
Ebenso wie die Regressionsanalyse beruht die Varianzanalyse auf dem Prinzip der Zerlegung der Varianz der abhängigen Variablen. Durch die Einteilung in Zellen wird die Gesamtvarianz geteilt in Varianz zwischen den Zellen und Varianz innerhalb der Zellen. Die Varianz zwischen den Zellen wird durch das Wirken der Faktoren erklärt, die Varianz innerhalb der Zellen wird zufälligen, nicht betrachteten Einflüssen zugeschrieben. Die Nullhypothese besagt, daß zwischen allen Zellen keine systematischen Unterschiede bestehen. Es wird das Verhältnis zwischen der erklärten Varianz zwischen den Zellen und der nicht erklärten Varianz innerhalb der Zellen betrachtet und berechnet, wie wahrscheinlich das vorliegende Verhältnis unter Voraussetzung der Nullhypothese ist. Liegt diese Wahrscheinlichkeit unter der vorgegebenen Irrtumswahrscheinlichkeit, so wird die Nullhypothese verworfen.
Im mehrfaktoriellen Fall können einerseits die einzelnen Faktoren Einflüsse auf die abhängigen Variablen ausüben (Haupteffekte), als auch die Wechselwirkung zwischen den Faktoren. Eine Wechselwirkung liegt vor, wenn die Faktoren nicht unabhängig voneinander sind, d. h., wenn ein Faktor einen anderen beeinflußt. In diesem Fall ist die Signifikanzprüfung der Haupteffekte problematisch, da sich ein Faktor je nach Vorliegen eines anderen Faktors anders auswirkt.
Besteht der Verdacht, daß die abhängigen Variablen nicht nur von den Faktoren, sondern auch von anderen Variablen beeinflußt werden, so können diese als Kovariate in die Analyse aufgenommen werden; in diesem Fall spricht man von einer Kovarianzanalyse. Dabei werden die Faktoren um die Einflüsse der Kovariaten korrigiert, nachdem diese mittels einer Regressionsanalyse bestimmt wurden.
Voraussetzung für die Varianzanalyse ist die Intervallskalierung der abhängigen Variablen und der Kovariaten, die Normalverteilung der abhängigen Variablen und die Homogenität der Varianzen zwischen den verschiedenen Faktorstufen. Letztere wird durch die Tests von Cochran und von Bartlett & Box geprüft, die jede abhängige Variable einzeln untersuchen. Im multivariaten Fall ist der Test von Box aussagekräftiger, der alle abhängigen Variablen gleichzeitig behandelt.
Da die Varianzanalyse nur eine Aussage darüber trifft, ob sich die betrachteten Zellen überhaupt signifikant voneinander unterscheiden, kann daraus nicht auf die Einflußstärke der einzelnen Faktoren geschlossen werden. Im univariaten Fall kann für eine diesbezügliche Aussage eine multiple Klassifikationsanalyse herangezogen werden. Sie berechnet die partielle Korrelation jedes Faktors mit der abhängigen Variablen bereinigt um die Einflüsse der anderen Faktoren und gibt außerdem durch das multiple Bestimmtheitsmaß an, wieviel Prozent der Varianz der abhängigen Variablen durch alle Faktoren gemeinsam erklärt wird.
Literatur: Röhr, Lohse & Ludwig, 1983, S. 262; Hartung & Elpelt, 1992, S. 655; Hartung, Elpelt & Klösener, 1993, S. 609; Bühl & Zöfel, 1995, S. 351; Backhaus, Erichson, Plinke & Weiber, 1996, S. 56; Fahrmeir, Hamerle & Nagl, 1996, S. 169; nur univariate Varianzanalyse: Janssen & Laatz, 1994, S. 305; ebenfalls: Brosius & Brosius, 1995, S. 417; nur einfaktorielle Varianzanalyse: Clauß, Finze & Partzsch, 1994, S. 326; nur multivariate mehrfaktorielle Varianzanalyse: Norušis, 1990, S. B-63.
3.2.8 Faktorenanalyse
Bei der Faktorenanalyse werden mehrere Variable zu möglichst homogenen Gruppen zusammengefaßt, sodaß je zwei Variable in der selben Gruppe stark, in zwei verschiedenen Gruppen jedoch nur schwach miteinander korrelieren. Abstrakt wird diese Gruppenbildung dadurch erklärt, daß hinter den Variablen sogenannte Faktoren liegen und die beobachteten Variablen nur mehr oder weniger gute Realisierungen des abstrakten Faktors sind. Im Normalfall geht man davon aus, daß die Faktoren voneinander unabhängig sind.
In der Psychologie beruhen beispielsweise zahlreiche Modelle der Intelligenz auf faktorenanalytischen Überlegungen. Dabei wurden zuerst die Leistungen von Versuchspersonen in mehreren dem jeweiligen Forscher relevant erscheinenden Aufgaben gemessen und diese dann zu abstrakten Faktoren wie Rechenleistung, Sprachgewandtheit, Gedächtnisleistung etc. zusammengefaßt.
Grafisch kann man sich das Verfahren der Faktorenanalyse folgendermaßen vorstellen: Die einzelnen Variablen werden als Vektoren aufgefaßt, wobei jede Versuchsperson einer Komponente entspricht; bei n Versuchspersonen sind die Vektoren also n-dimensional. Die Korrelation zwischen zwei Variablen entspricht dann dem Kosinus des eingeschlossenen Winkels. Da die Variablen sinnvollerweise untereinander korreliert sind, sind nicht alle Winkeln rechte Winkeln; daher spannen die Vektoren nur einen Raum mit weniger als n Dimensionen auf, beispielsweise k. Die Faktoren sind nun die Achsen dieses k-dimensionalen Raumes, dementsprechend läßt sich jede Variable als Linearkombination der Faktoren darstellen. Nun können für jede Variable ihre Faktorladungen ermittelt werden, das sind die Korrelationen der Variablen mit jedem Faktor. Bei einer geglückten Faktorenanalyse lädt jede Variable in genau einen Faktor hoch, in alle anderen nur niedrig.
Um die Interpretierbarkeit der Faktoren zu erhöhen, können diese rotiert werden, d. h., die Achsen des k-dimensionalen Raumes werden so gedreht, daß sie sich möglichst gut an die Variablen-Vektoren anpassen. Dadurch ändern sich die Faktorladungen in die gewünschte Richtung, sodaß jede Variable mit genau einem Faktor stark korreliert.
Das eigentliche Problem bei der Faktorenanalyse besteht in der Bestimmung der Anzahl der Faktoren. Als Faustregel gilt, daß nur jene Faktoren sinnvoll sind, deren Eigenwert größer als 1 ist, da der Faktor sonst weniger Gesamtvarianz erklärt als eine einzelne Variable. Will man jedoch nicht alle Faktoren mit Eigenwert größer 1 aufnehmen, so empfiehlt es sich, bei jenem Faktor aufzuhören, nach dem die Größe der Eigenwerte deutlich absinkt.
Als Abschluß der Faktorenanalyse können für jede einzelne Versuchsperson die sogenannten Faktorwerte berechnet werden, das sind standardisierte Werte, die die Ausprägung jedes einzelnen Faktors bei jeder Person angeben. Dadurch entstehen bei k Faktoren k neue Variable, die für weitere Berechnungen verwendet werden können.
Es gibt mehrere Prüfgrößen, die angeben, wie gut das vorliegende Datenmaterial für eine Faktorenanalyse geeignet ist. Der Bartlett-Test auf Sphärizität testet die Nullhypothese, daß alle Korrelationen zwischen den Variablen in der Grundgesamtheit null sind, wodurch eine Faktorenanalyse nicht sinnvoll wäre. Der Test von Kaiser, Meyer & Olkin untersucht die partiellen Korrelationen zwischen je zwei Variablen und errechnet daraus eine Kennzahl für die Eignung der vorliegenden Variablen für eine Faktorenanalyse. Das Maß schwankt zwischen 0 und 1, bei Werten unter 0,5 ist eine Faktorenanalyse inakzeptabel, über 0,8 ist die Eignung gut.
Literatur: Diehl & Kohr, 1991, S. 338; Hartung & Elpelt, 1992, S. 505; Norušis, 1992, S. 47; Clauß, Finze & Partzsch, 1994, S. 302; Brosius & Brosius, 1995, S. 815; Bühl & Zöfel, 1995, S. 367; Backhaus, Erichson, Plinke & Weiber, 1996, S. 190; Brachinger & Ost, 1996, S. 639.
3.2.9 Korrektur der Irrtumswahrscheinlichkeit
Wenn mehrere Signifikanzprüfungen unabhängig voneinander durchgeführt werden, steigt die Wahrscheinlichkeit einer zufälligen Signifikanz mit der Anzahl der Prüfungen an. Diese sogenannte Alpha-Fehler-Inflation kann jedoch durch Anpassung der Irrtumswahrscheinlichkeit α an die Anzahl der Tests vermieden werden.
Die Wahrscheinlichkeit, bei einem Test die Nullhypothese abzulehnen, obwohl
sie in Wirklichkeit zutrifft, ist definitionsgemäß α. Dementsprechend ist die Wahrscheinlichkeit, daß die Nullhypothese abgelehnt
wird, wenn sie tatsächlich nicht zutrifft (1–α)
. Werden n voneinander unabhängige Tests mit Irrtumswahrscheinlichkeit
α* durchgeführt, so ist diese Wahrscheinlichkeit (1–α*)n
; die Irrtumswahrscheinlichkeit, daß die Nullhypothese mindestens einmal
fälschlicherweise abgelehnt wird, ist dann die Gegenwahrscheinlichkeit
von (1–α*)n,
nämlich 1–(1–α*)n
. Um Aussagen mit der üblichen Irrtumswahrscheinlichkeit α
treffen zu können, muß α* also so gewählt werden, daß 1–(1–α*)n=α
gilt, d. h. (1–α*)n=1–α,
also ![]() und schließlich:
und schließlich: ![]() .
.
Um also bei n unabhängigen Tests insgesamt eine Irrtumswahrscheinlichkeit
von α zu erzielen,
muß jeder dieser Tests mit einer Irrtumswahrscheinlichkeit von ![]() durchgeführt werden.
durchgeführt werden.
Literatur: Fischer, 1992, S. 202.
4 Die Ergebnisse
4.1 Erläuterungen
Der Fragebogen umfaßt 70 Variable; diese sind im folgenden einzeln dargestellt. Zusätzlich habe ich einige neue Variable aus den bestehenden errechnet; diese befinden sich hinter der letzten zugrundeliegenden Variablen. Zur besseren Unterscheidbarkeit sind jene Überschriften, die wörtlich den Fragen im Fragebogen entsprechen, in Anführungszeichen geschrieben.
Die Säulendiagramme geben im allgemeinen die Verteilung auf die Antwortalternativen in Prozent an; zur besseren Vergleichbarkeit habe ich alle auf 100% skaliert. Von-Bis-Werte habe ich dabei halb-halb zugeteilt, d. h., bei der Antwort „2 bis 3“ wurde beispielsweise 0,5 zu 2 und 0,5 zu 3 gezählt. Durch diese Aufteilung sind die Säulendiagramme übersichtlicher und besser vergleichbar. Die genaue Verteilung der Antworten ist aus den Tabellen ersichtlich.
Die Kreisdiagramme zeigen den Anteil der gültigen Antworten in Prozent, also jenen Anteil, dessen Verteilung im dazugehörigen Säulendiagramm dargestellt ist. Dabei gilt folgende Legende:

Grundsätzlich habe ich jede Variable auf Unterschiede zwischen Schülern mit „positiver“ und „negativer“ Jahreszeugnisnote, zwischen Unter-15jährigen und Ab-15jährigen, zwischen männlichen und weiblichen Schülern sowie zwischen Schülern aus AHS und BHS untersucht. Bei letzterer Trennung habe ich selbstverständlich nur Schüler ab der 9. Schulstufe betrachtet. Die Bezeichnungen „jüngere“ und „ältere Schüler“ bezieht sich auf Unter-15jährige und Ab-15jährige.
Ergebnisse mit Irrtumswahrscheinlichkeit unter 0,05 bezeichne ich als „signifikant“, unter 0,01 als „hoch signifikant“ und unter 0,001 als „höchst signifikant“.
4.2 Die Variablen im einzelnen
„1) Was waren Deine Noten in Mathematik im abgelaufenen Schuljahr?“
„1. Schularbeit“
| Note: | 1 | 2 | 3 | 4 | 4,5 | 5 | n.b. | vers. | gestr. | k.A. |
|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 2 | 22 | 49 | 125 | 1 | 185 | 0 | 3 | 1 | 13 |
| Prozent i | 0,5 | 5,5 | 12,2 | 31,2 | 0,2 | 46,1 | 0 | 0,7 | 0,2 | 3,2 |
| Prozent g | 0,5 | 5,7 | 12,8 | 32,6 | 0,3 | 48,2 |
„2. Schularbeit“

| Note: | 1 | 2 | 2,5 | 3 | 4 | 4,5 | 5 | n.b. | vers. | gestr. | k.A. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 1 | 6 | 1 | 41 | 107 | 1 | 212 | 0 | 6 | 12 | 14 |
| Prozent i | 0,2 | 1,5 | 0,2 | 10,2 | 26,7 | 0,2 | 52,9 | 0 | 1,5 | 3 | 3,5 |
| Prozent g | 0,3 | 1,6 | 0,3 | 11,1 | 29 | 0,3 | 57,5 |
„3. Schularbeit“
| Note: | 1 | 2 | 3 | 4 | 5 | n.b. | vers. | gestr. | k.A. |
|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 0 | 4 | 27 | 78 | 199 | 2 | 10 | 44 | 37 |
| Prozent i | 0 | 1 | 6,7 | 19,5 | 49,6 | 0,5 | 2,5 | 11 | 9,2 |
| Prozent g | 0 | 1,3 | 8,8 | 25,3 | 64,6 |
„Halbjahreszeugnis“
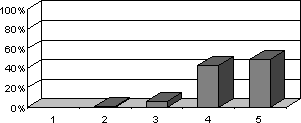
| Note: | 1 | 2 | 3 | 4 | 4,5 | 5 | n.b. | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 0 | 5 | 22 | 158 | 1 | 181 | 0 | 34 |
| Prozent i | 0 | 1,2 | 5,5 | 39,4 | 0,2 | 45,1 | 0 | 8,5 |
| Prozent g | 0 | 1,4 | 6 | 43,1 | 0,3 | 49,3 |
„4. Schularbeit“
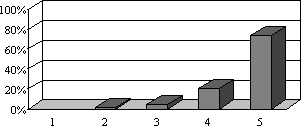
| Note: | 1 | 2 | 3 | 4 | 5 | n.b. | vers. | gestr. | k.A. |
|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 0 | 4 | 16 | 77 | 270 | 3 | 10 | 1 | 20 |
| Prozent i | 0 | 1 | 4 | 19,2 | 67,3 | 0,7 | 2,5 | 0,2 | 5 |
| Prozent g | 0 | 1,1 | 4,4 | 21 | 73,6 |
„5. Schularbeit“
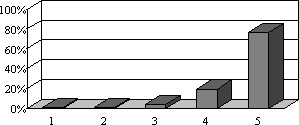

| Note: | 1 | 2 | 3 | 4 | 4,5 | 5 | n.b. | vers. | gestr. | k.A. |
|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 1 | 2 | 13 | 65 | 2 | 260 | 1 | 7 | 22 | 28 |
| Prozent i | 0,2 | 0,5 | 3,2 | 16,2 | 0,5 | 64,8 | 0,2 | 1,7 | 5,5 | 7 |
| Prozent g | 0,3 | 0,6 | 3,8 | 19 | 0,6 | 75,8 |
„6. Schularbeit“
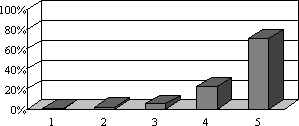
| Note: | 1 | 2 | 3 | 4 | 5 | n.b. | vers. | gestr. | k.A. |
|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 1 | 3 | 8 | 37 | 118 | 3 | 5 | 106 | 120 |
| Prozent i | 0,2 | 0,7 | 2 | 9,2 | 29,4 | 0,7 | 1,2 | 26,4 | 29,9 |
| Prozent g | 0,6 | 1,8 | 4,8 | 22,2 | 70,7 |
„Jahreszeugnis“
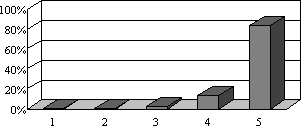

| Note: | 1 | 2 | 3 | 4 | 4,5 | 5 | n.b. | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 1 | 2 | 8 | 49 | 1 | 308 | 1 | 31 |
| Prozent i | 0,2 | 0,5 | 2 | 12,2 | 0,2 | 76,8 | 0,2 | 7,7 |
| Prozent g | 0,3 | 0,5 | 2,2 | 13,3 | 0,3 | 83,5 |
Notendurchschnitt aller Schularbeiten und Zeugnisse
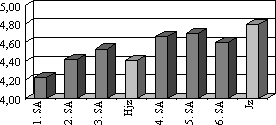
| 1.SA | 2.SA | 3.SA | Hjz | 4.SA | 5.SA | 6.SA | Jz | |
|---|---|---|---|---|---|---|---|---|
| Schnitt | 4,23 | 4,42 | 4,53 | 4,41 | 4,67 | 4,7 | 4,61 | 4,8 |
| Prozent g | 95,8 | 92 | 76,8 | 91,5 | 91,5 | 85,5 | 41,6 | 92 |
Bei Betrachtung aller sechs Schularbeiten fällt auf, daß der Notendurchschnitt bis zur 5. Schularbeit kontinuierlich abfällt, während er bei der 6. wieder leicht ansteigt. Diese Leistungsschwankung könnte dadurch verursacht werden, daß bei den Schülern im Verlauf des Schuljahres die Motivation zurückgeht, wohingegen sie sich bei der letzten Schularbeit noch einmal vermehrt anstrengen.
Der Vergleich der beiden Zeugnisse zeigt bereits auf den ersten Blick, daß das Jahreszeugnis deutlich schlechter ausfällt als das Halbjahreszeugnis.
Besonders interessiert hat mich die Frage, inwieweit sich die Zeugnisnoten aus den Schularbeitsnoten vorhersagen lassen. Die Lösung dieses Problems war methodisch schwierig: Das eigentlich dafür geschaffene Verfahren – die multiple Regressionsanalyse – setzt Intervallskalenniveau voraus, das Schulnoten nicht aufweisen (siehe Seite 37), während das methodisch zulässige Verfahren – die multiple Rangkorrelation – nur den Zusammenhang zwischen den Noten mißt, ohne die Frage der Einflußstärke der einzelnen Schularbeiten zu beantworten. Genaugenommen trifft die Korrelation sogar nur eine Aussage über die Gemeinsamkeiten der Variablen, nicht jedoch über die Richtung des Einflusses. Dieser Mangel ist jedoch in diesem Zusammenhang irrelevant, da aufgrund der zeitlichen Abfolge nur eine Beeinflussung des Zeugnisses durch die Schularbeiten (und nicht eine Beeinflussung der Schularbeiten durch das Zeugnis) in Frage kommt.
Ich habe zuerst die multiple Rangkorrelation berechnet, um einen ersten Eindruck zu gewinnen, ob überhaupt ein Zusammenhang vorliegt. Aufgrund der geringen Schwankung der Zeugnisnoten (im Jahreszeugnis haben rund 80% die Note „5“) wäre eigentlich zu erwarten, daß die Korrelation gering ist; tatsächlich fällt sie jedoch mit 0,67 erstaunlich hoch aus.
Eine exakte Signifikanzprüfung dieser Korrelation ist zwar nicht möglich (vgl. Röhr, Lohse & Ludwig, 1983, S. 213), aus der Größe der Korrelation und dem Stichprobenumfang kann jedoch auch mit freiem Auge erkannt werden, daß eine hohe Signifikanz gegeben ist.
Ausgehend von diesem Ergebnis wollte ich die Regressionsgleichung ermitteln, da diese einerseits Aufschluß über die Einflußstärke der einzelnen Schularbeiten gibt, und andererseits – was mir noch wichtiger war – jedem die Möglichkeit bietet, den gefundenen Zusammenhang an seinen eigenen Noten zu überprüfen.
Die Ordinalskalierung der Variablen ist zwar nach wie vor problematisch, durch die eindeutigen Ergebnisse der multiplen Rangkorrelation halte ich jedoch die Gefahr für beschränkt, daß die Regressionsanalyse aufgrund des mangelnden Skalenniveaus nur Scheinzusammenhänge ausweist. Trotzdem möchte ich nochmals darauf hinweisen, daß sämtliche Ergebnisse der Regressionsanalyse mit Vorsicht zu genießen sind.
Die weiteren Voraussetzungen einer Regressionsanalyse sind jedenfalls durchwegs gut erfüllt: Die Toleranz liegt bei allen Variablen über 0,6, der Konditionsindex bei allen Eigenwerten unter 0,26 und der größte Teile der Varianz jeder Variablen wird einem andern Eigenwert zugeordnet, was insgesamt dafür spricht, daß keine Kollinearität vorliegt. Auch die Unabhängigkeit der Residuen scheint gegeben zu sein, da sowohl der Durbin & Watson-Koeffizient mit 2,24 im zulässigen Bereich liegt, als auch die grafische Überprüfung der Residuen keine deutliche Abweichung von der Normalverteilung gezeigt hat.
Allerdings ergab sich ein anderes Problem, das in den erhobenen Daten seinen
Ursprung hat: Es konnten nur 130 Fragebögen (32,4%) in die Regressionsanalyse
aufgenommen werden, da bei allen anderen die Angabe mindestens einer Note fehlte.
Der überwiegende Großteil ging durch das Fehlen der 6. Schularbeitsnote
verloren. Das ist darauf zurückzuführen, daß in vielen Klassen
nur fünf oder noch weniger Mathematikschularbeiten abgehalten werden, was
auch relativ viele Schüler durch Streichung der 6. Schularbeit bestätigt
haben.
Inhaltlich heißt das allerdings, daß die gefundene Regressionsgleichung
nur für Klassen mit sechs Schularbeiten anwendbar ist.
Die Regressionsanalyse lieferte folgende Ergebnisse:
Das korrigierte multiple Bestimmtheitsmaß ist mit 0,73 erstaunlich hoch,
da dies bedeuten würde, daß 73% der Varianz der Jahreszeugnisnote
allein durch die Schularbeiten erklärt wird. Dieser Wert ist höchst
signifikant.
Die ermittelte Regressionsgleichung lautet:
J = 0,103·S1 + 0,034·S2 + 0,026·S3
+ 0,217·S4 + 0,165·S5 + 0,440·S6
+ 0,275 .
Dabei steht J für die Jahreszeugnisnote und Si für die
Note der i-ten Schularbeit.
Durch Vergleich der sechs Regressionskoeffizienten ergibt sich folgendes Bild: Die 6. Schularbeit hat den weitaus größten Einfluß auf die Jahreszeugnisnote, gefolgt von der 4., 5. und 1. Fast bedeutungslos ist hingegen die 2. und 3. Schularbeit. Die Signifikanzprüfung verstärkt diesen Eindruck: Der Einfluß der 6. und 4. Schularbeit ist höchst signifikant, jener der 5. und 1. hoch signifikant, wohingegen sich die 2. und 3. Schularbeit nicht signifikant auswirkt. Der niedrige konstante Koeffizient spricht dafür, daß die Gleichung nicht nur für Schüler mit schlechten Noten gilt, da bei entsprechend guten Schularbeitsnoten auch eine gute Zeugnisnote möglich ist. Der konstante Koeffizient ist zudem nicht signifikant.
Um auch für Klassen mit nur fünf Schularbeiten Aussagen treffen zu können, habe ich in einer zweiten Regressionsanalyse nur jene Personen betrachtet, die die 6. Schularbeit gestrichen haben. Das sind zwar 106 Personen (26,4%), allerdings konnten aufgrund fehlender Daten in den anderen Variablen nur 52 (13,0%) in die Analyse aufgenommen werden.
Dabei ergab sich schon bei der Prüfung der Voraussetzungen ein schlechteres Bild als bei der ersten: Die Toleranz ist zwar mit stets mehr als 0,88 noch größer als oben und auch die Zuordnung der Varianz der Variablen zu den Eigenwerten ist sehr zufriedenstellend, der größte Konditionsindex ist jedoch mit 47 eindeutig zu groß, um Kollinearität mit großer Wahrscheinlichkeit ausschließen zu können. Ähnlich zwiespältig zeigt sich die Überprüfung der Unabhängigkeit der Residuen: Der Durbin & Watson-Koeffizient ist zwar mit 2,18 ebenfalls besser als oben, die Abweichung von der Normalverteilung in den Diagrammen erschien mir aber augenfällig.
Die Ergebnisse lassen zudem auch stark zu wünschen übrig:
Der Gesamteinfluß der Schularbeiten ist zwar signifikant, jedoch ist das
korrigierte Bestimmtheitsmaß mit 0,16 zu gering, um von einem brauchbaren
Modell zu sprechen.
Ebenso die Regressionsgleichung:
J = –0,033·S1 + 0,000·S2 + 0,180·S3
+ 0,129·S4 + 0,112·S5 + 3,051 .
Der negative Koeffizient bei der 1. Schularbeit würde nämlich bedeuten, daß sich eine gute Note negativ auf das Jahreszeugnis auswirkt, was aus inhaltlichen Gründen jedoch zumindest stark bezweifelt werden muß. Außerdem folgt aus dem konstanten Koeffizienten, daß bessere Noten als „3“ nicht möglich sind, da alle anderen Koeffizienten entweder positiv oder verschwindend klein sind.
Insgesamt muß die diese zweite Regressionsanalyse als gescheitert betrachtet werden; für Klassen mit nur fünf Schularbeiten läßt sich aus den vorliegenden Daten also keine Aussage gewinnen.
Schließlich habe ich noch den Zusammenhang zwischen dem Halbjahreszeugnis und den ersten drei Schularbeiten untersucht. Die multiple Rangkorrelation beträgt 0,59, was eine weitere Erforschung durch eine Regressionsanalyse meines Erachtens abermals rechtfertigt.
Dieses Mal konnten 278 Fragebögen (69,3%) in die Analyse aufgenommen werden; analog zu oben wurde der größte Ausfall durch die 3. Schularbeit verursacht.
Die Voraussetzungen sind größtenteils gut erfüllt: Die Toleranz liegt stets über 0,78, der Konditionsindex unter 18 und auch die Zuordnung des größten Teils der Varianz erfolgt für jede unabhängige Variable zu einem anderen Eigenwert. Der Durbin & Watson-Koeffizient ist mit 2,09 sogar sehr gut, allerdings ist die grafische Anpassung an die Normalverteilung nicht ganz überzeugend.
Das korrigierte multiple Bestimmtheitsmaß ist mit 0,59 zwar geringer
als oben, das Modell ist aber dennoch höchst signifikant. Die Regressionsgleichung
lautet:
H = 0,286·S1 + 0,234·S2 + 0,300·S3
+ 0,813 .
Dabei steht H für die Halbjahreszeugnisnote.
Alle vier Koeffizienten sind höchst signifikant. Die Gleichung erscheint zwar inhaltlich sehr plausibel, da alle drei Schularbeiten einen annähernd gleich starken Einfluß haben, dürfte jedoch nur für Schüler mit schlechten Noten gelten, da durch den hohen konstanten Koeffizienten gute Noten kaum möglich sind.
Zur weiteren Erforschung dieses Zusammenhanges wäre eine repräsentative (und nicht wie in diesem Fall auf leistungsschwache Schüler beschränkte) Untersuchung notwendig. Dabei würde ich aufgrund der größeren Schwankung der Noten sogar höhere Korrelationen und bessere Regressionsgleichungen erwarten, da es „eine weitverbreitete Praxis ist, vor allem die Schularbeitsnoten als Grundlage für die Zeugnisnote heranzuziehen.“(Hanisch, 1990, S. 231).
„2) Welche Note würdest Du Dir selbst im Jahreszeugnis geben?“
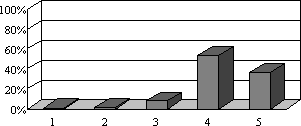

| Note: | 1 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 4 | 5 | 1 | 29 | 2 | 210 | 1 | 145 | 4 |
| Prozent i | 1 | 1,2 | 0,2 | 7,2 | 0,5 | 52,4 | 0,2 | 36,2 | 1 |
| Prozent g | 1 | 1,3 | 0,3 | 7,3 | 0,5 | 52,9 | 0,3 | 36,5 |
Eine isolierte Interpretation der selbst gegebenen Jahreszeugnisnote erscheint mir nicht zweckmäßig, da sinnvolle Schlüsse wohl nur in Verbindung mit der tatsächlichen Note gezogen werden können.
Differenz zwischen tatsächlicher und selbst gegebener Note im Jahreszeugnis (in Notenstufen)
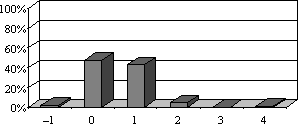

| Wert: | –1 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 4 | k.A. |
|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 9 | 173 | 2 | 156 | 2 | 16 | 1 | 2 | 4 | 36 |
| Prozent i | 2,2 | 43,1 | 0,5 | 38,9 | 0,5 | 4 | 0,2 | 0,5 | 1 | 9 |
| Prozent g | 2,5 | 47,4 | 0,5 | 42,7 | 0,5 | 4,4 | 0,3 | 0,5 | 1,1 |
Der auf den ersten Blick entstehende Eindruck, daß die Schülernote mit der Lehrernote im großen und ganzen recht gut übereinstimmt (immerhin würden sich knapp die Hälfte der Schüler die selbe Note geben, die sie tatsächlich bekommen haben), trügt. Die Trennung der Schüler in solche mit „positiver“ und solche mit „negativer“ Jahreszeugnisnote bringt nämlich deutliche Unterschiede zutage:
…bei „positiver“ Jahreszeugnisnote
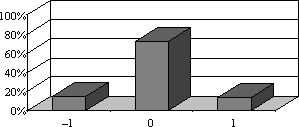
| Wert: | –1 | 0 | 1 | k.A. |
|---|---|---|---|---|
| Anzahl | 9 | 43 | 8 | 0 |
| Prozent i | 2,2 | 10,7 | 2 | 0 |
| Prozent g | 15 | 71,7 | 13,3 |
…bei „negativer“ Jahreszeugnisnote
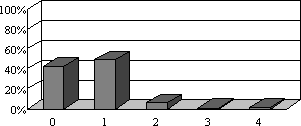
| Wert: | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 4 | k.A. |
|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 130 | 1 | 148 | 2 | 16 | 1 | 2 | 4 | 4 |
| Prozent i | 32,4 | 0,2 | 36,9 | 0,5 | 4 | 0,2 | 0,5 | 1 | 1 |
| Prozent g | 42,8 | 0,3 | 48,7 | 0,7 | 5,3 | 0,3 | 0,7 | 1,3 |
Die Unterschiede zwischen diesen beiden Gruppen sind augenfällig: Während sich die Schüler mit „positiver“ Jahreszeugnisnote mit überwiegender Mehrheit die selbe Note wie der Lehrer geben würden, sehen sich jene mit „negativer“ Zeugnisnote mehrheitlich besser als der Lehrer.
Dieses Ergebnis steht in krassem Gegensatz zur Literatur, in der einhellig von stets großer Übereinstimmung zwischen Schüler- und Lehrernoten berichtet wird (vgl. Seyfried, 1980, zitiert nach Weiss, 1989 a, S. 106; Viebahn, 1982, S. 64). So schreibt beispielsweise Winter: „Freilich benoten sich die Schüler überwiegend so, wie der Lehrer dies täte […]. Die Abweichungen sind meistens gering.“ (Winter, 1991, S. 169). Ich führe die unterschiedlichen Ergebnisse darauf zurück, daß bei diesen Untersuchungen Schüler aller Leistungsstärken befragt wurden, wohingegen sich die vorliegende Befragung speziell an Leistungsschwache richtete, bei denen sich aber gerade die stärkeren Abweichungen zeigen.
Diese Erklärungsmöglichkeit fällt allerdings bei den Ergebnissen von Mies-Suermann weg: Sie untersuchte in ihrer Erhebung unter 158 Nürnberger Schülerinnen des 7. Schuljahres im Schuljahr 1972/73 unter anderem, ob sich die Schülerinnen von ihren Lehrern gerecht beurteilt fühlen. Dabei gab die überwiegende Mehrheit an, zumindest von den meisten Lehrern gerecht beurteilt worden zu sein. „Dabei ließen sich zwischen guten und schlechten Schülern keine Unterschiede feststellen“ (Mies-Suermann, 1975, S. 146).
Um festzustellen, ob auch zwischen den Geschlechtern, Schularten und Altersgruppen deutliche Unterschiede bestehen, habe ich die entsprechenden Kreuztabellen betrachtet. Dabei zeigten sich nach Alter und Schulart nur verschwindende Differenzen, nach dem Geschlecht jedoch größere, sodaß mir bezüglich dieses Faktors eine weitere Analyse sinnvoll erschien, bezüglich der beiden anderen hingegen nicht.
Ich habe also eine univariate mehrfaktorielle Varianzanalyse mit der Differenz zwischen tatsächlicher und selbst gegebener Jahreszeugnisnote als abhängiger Variable und dem Geschlecht und der Jahreszeugnisnote als Faktoren durchgeführt.
Daß die abhängige Variable intervallskaliert ist, kann angenommen werden, da es sich nicht um Schulnoten, sondern um die Differenz zwischen Schulnoten handelt. Die Anpassung der Meßwerte an die Normalverteilung habe ich grafisch durch Histogramme überprüft, und sie schien mir in allen vier Zellen im großen und ganzen vertretbar. Die Unterschiede zwischen den Varianzen werden jedoch von den Tests von Cochran und Bartlett & Box als höchst signifikant ausgewiesen, wodurch eine der Voraussetzungen für die Varianzanalyse jedenfalls nicht erfüllt ist.
Somit stellt sich natürlich die Frage, ob die Durchführung einer Varianzanalyse überhaupt zulässig ist. In der statistischen Praxis wird diese Frage in ähnlich gelagerten Fällen zumeist bejaht, da einerseits die meisten Verfahren gegenüber Verletzungen ihrer Voraussetzungen relativ robust sind, und es andererseits oft keine brauchbaren Alternativen gibt. Im vorliegenden konkreten Fall ist eine Signifikanzprüfung zwar auch durch zwei t-Tests möglich, allerdings erhöht sich das Risiko einer Scheinsignifikanz mit zunehmender Anzahl der durchgeführten Tests schnell, sodaß diese Alternative bei mehreren Faktoren und mehreren abhängigen Variablen zunehmend problematisch wird.
Die Ergebnisse der Varianzanalyse entsprechen voll den Erwartungen:
Insgesamt bestehen höchst signifikante Unterschiede zwischen den Zellen.
Der Einfluß von Wechselwirkungen ist nicht signifikant, jener der Haupteffekte
hingegen höchst signifikant, und zwar wirkt sich die Jahreszeugnisnote
höchst signifikant, das Geschlecht hoch signifikant aus.
Die multiple Klassifikationsanalyse zum Vergleich der Einflußstärken zeigt ein ähnliches Bild: Die partielle Korrelation der abhängigen Variable mit der Jahreszeugnisnote beträgt 0,34, jene mit dem Geschlecht 0,13. Das multiple Bestimmtheitsmaß liegt bei 0,14, es werden also insgesamt 14% der Varianz der abhängigen Variablen durch die beiden Faktoren erklärt.
Die Unterschiede zwischen den Geschlechtern gehen in die Richtung, daß sich männliche Schüler im Vergleich zur tatsächlichen Note etwas besser beurteilen würden als weibliche, allerdings ist der Unterschied zwischen den Mittelwerten mit 0,21 nicht sehr groß. Zum Vergleich: Die Mittelwertdifferenz zwischen Schülern mit „positiver“ und solchen mit „negativer“ Jahreszeugnisnote beträgt 0,70 (die Mittelwerte sind –0,02 und 0,68).
Aufgrund der Verletzungen der Voraussetzungen der Varianzanalyse habe ich die Signifikanzprüfung durch zwei t-Tests wiederholt, allerdings unter Anpassung der Irrtumswahrscheinlichkeit an die Tatsache, daß zwei Tests parallel durchgeführt werden. Für die korrigierte Irrtumswahrscheinlichkeit für Aussagen auf dem 95%-Signifikanzniveau ergibt sich 0,025.
Die Differenzen nach dem Geschlecht zeigten sich auch hier signifikant, jene nach der Jahreszeugnisnote sogar höchst signifikant.
„3) Welche Note würdest Du Deinem/r Mathematiklehrer/in geben?“
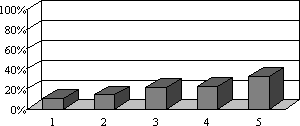

| Note: | 1 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 40 | 54 | 1 | 83 | 4 | 85 | 2 | 125 | 7 |
| Prozent i | 10 | 13,5 | 0,2 | 20,7 | 1 | 21,2 | 0,5 | 31,2 | 1,7 |
| Prozent g | 10,2 | 13,7 | 0,3 | 21,1 | 1 | 21,6 | 0,5 | 31,7 |
Die Noten für die Mathematiklehrer sind besser als erwartet, allerdings zeigt auch hier die Unterteilung nach der Jahreszeugnisnote deutliche Unterschiede: Die durchschnittliche Lehrernote liegt bei den Schülern, die im Zeugnis „positiv“ waren, mit 2,93 um 0,69 Notenstufen unter jenem der Schüler, die „negativ“ waren (3,62).
Kreuztabellen zeigten nur geringe Unterschiede nach Geschlecht und Alter; die Mittelwerte differieren jeweils um weniger als 0,2. Beim Vergleich der AHS-Oberstufe mit den BHS traten hingegen deutlichere Abweichungen zutage, sodaß mir eine Signifikanzprüfung gerechtfertigt erschien.
Zur simultanen Prüfung der beiden Faktoren Jahreszeugnisnote und Schulart
wäre zwar eine univariate zweifaktorielle Varianzanalyse an sich geeignet,
diese ist hier allerdings gleich aus mehreren Gründen abzulehnen: Die abhängige
Variable ist lediglich ordinalskaliert, die Meßwerte sind offensichtlich
nicht normalverteilt und für den Vergleich der AHS-Oberstufe mit den BHS
müßte die Stichprobe auf Oberstufenschüler eingeschränkt
werden.
Daher habe ich zwei U-Tests mit Korrektur der Irrtumswahrscheinlichkeit vorgezogen.
Diese weisen den Unterschied nach der Jahreszeugnisnote als höchst signifikant,
jenen zwischen den Schularten jedoch als nicht signifikant aus.
Es hat mich die Frage interessiert, inwieweit die Note für den Lehrer von „äußeren Umständen“ beeinflußt wird. Nach meinen Überlegungen kommen dafür hauptsächlich folgende in Frage, und zwar aus den angeführten Gründen:
- die Jahreszeugnisnote: Die Schüler „rächen“ sich für die eigene schlechte Note mit einer ebensolchen Beurteilung für den Lehrer.
- die Differenz zwischen tatsächlicher und selbst gegebener Jahreszeugnisnote: Die Schüler geben eine umso schlechtere Note, je ungerechter sie sich selbst beurteilt fühlen.
- der Anteil von Schülern mit Wiederholungsprüfung in Mathematik an der Klassenschülerzahl (Frage 8 und 9): Ein Lehrer wird umso schlechter benotet, je mehr Schüler eine Wiederholungsprüfung haben.
Hier ergibt sich das gleiche methodische Problem wie bei der Berechnung der Abhängigkeit der Jahreszeugnisnote von den Schularbeitsnoten (Frage 1): Das dafür besser geeignete Verfahren der Regressionsanalyse darf aufgrund des mangelnden Skalenniveaus strenggenommen nicht verwendet werden, wohingegen das methodisch zulässige Verfahren der Rangkorrelation kein so klares Ergebnis liefert.
Ich habe daher eine ähnliche Vorgangsweise wie bei Frage 1 gewählt: Zuerst habe ich durch die Rangkorrelation überprüft, welche der in Frage kommenden Variablen sich signifikant auf die Lehrernote auswirken und mit diesen anschließend eine Regressionsanalyse durchgeführt.
Überraschenderweise waren tatsächlich alle drei Korrelationen hoch signifikant, allerdings mit Koeffizienten von 0,14 bis 0,16 durchwegs niedrig.
Die anderen Voraussetzungen für die Regressionsanalyse sind gut erfüllt: Die Toleranz liegt bei allen Variablen über 0,88, der Konditionsindex bei allen Eigenwerten unter 25 und auch die Verteilung der Varianz auf die Eigenwerte ist sehr gut. Außerdem zeigt ein grafischer Vergleich der Residuen mit der Normalverteilung keine allzu große Abweichung und der Durbin & Watson-Koeffizient liegt mit 2,14 klar im zulässigen Bereich.
Die Regressionsanalyse weist den Einfluß der drei unabhängigen Variablen zwar als höchst signifikant aus, das korrigierte multiple Bestimmtheitsmaß ist mit 0,06 allerdings verschwindend gering. Von den drei unabhängigen Variablen hat das Verhältnis von Schülern mit Wiederholungsprüfung in Mathematik an der Klassenschülerzahl bei einem standardisierten Regressionskoeffizienten von 0,18 einen hoch signifikanten Einfluß, die Jahreszeugnisnote bei einem Koeffizienten von 0,12 einen signifikanten, wohingegen sich die Differenz zwischen tatsächlicher und selbst gegebener Jahreszeugnisnote nicht signifikant auf die Lehrernote auswirkt.
Ich halte dieses Ergebnis auch politisch für interessant, wird doch von den Gegnern der Lehrerbeurteilung durch Schüler immer wieder angeführt, daß Schüler nicht reif genug seien, ein fundiertes Urteil abzugeben und sie sich zu stark von persönlichen Motiven (allen voran „Rache“ für die eigene Note) leiten ließen. Ob die Noten für die Lehrer auf fundierten Überlegungen beruhen, kann aus dem vorhandenen Datenmaterial natürlich nicht entschieden werden, jedoch kann man aufgrund der obigen Ergebnisse mit großer Sicherheit ausschließen, daß die Schüler stark von den drei betrachteten „persönlichen“ Motiven beeinflußt werden, da diese alle zusammen nur 6% der Varianz der Lehrernote erklären.
Da die eben erwähnten Argumente vor allem für jüngere Schüler ins Treffen geführt werden, habe ich dieselben Analysen eingeschränkt auf die Gruppe der Unter-15jährigen wiederholt. Damit wollte ich den beiden möglichen Kritikpunkten begegnen, daß erstens die Beeinflussung bei den jüngeren Schülern zwar stark sei, jedoch durch gemeinsame Betrachtung mit den älteren Schülern überlagert werde, oder zweitens junge und alte Schüler jeweils von anderen Motiven gelenkt werden, die einander aber gegenseitig aufheben.
Die Betrachtung der Korrelationskoeffizienten zeigt, daß nur mehr die Jahreszeugnisnote und die Differenz zwischen tatsächlicher und selbst gegebener Jahreszeugnisnote mit Koeffizienten von 0,25 und 0,29 hoch signifikant mit der Lehrernote korrelieren. Der Koeffizient mit dem Anteil der Schüler mit Wiederholungsprüfung ist hingegen mit 0,11 nicht signifikant. Aus diesem Grund habe ich die Regressionsanalyse auf die beiden ersten Variablen beschränkt.
Die Voraussetzungen sind gut erfüllt: Die Toleranz liegt durchwegs über 0,83, der Konditionsindex unter 17, die Verteilung der Varianz auf die Eigenwerte ist sehr gut, der Durbin & Watson-Koeffizient liegt mit 2,34 im zulässigen Bereich, lediglich die Normalverteilung der Residuen ist nicht ganz überzeugend.
Der Einfluß der beiden Variablen ist höchst signifikant, das korrigierte multiple Bestimmtheitsmaß beträgt jedoch auch hier nur 0,12. Einzeln wirkt sich nur die Differenz zwischen tatsächlicher und selbst gegebener Jahreszeugnisnote bei einem standardisierten Regressionskoeffizienten von 0,26 hoch signifikant auf die Lehrernote aus; die Jahreszeugnisnote hat keinen signifikanten Einfluß.
Aufgrund der Unterschiede zwischen den jungen und allen Schülern sah ich mich veranlaßt, eine dritte Analyse in der Gruppe der Ab-15jährigen durchzuführen um sicherzugehen, daß auch hier keine der betrachteten Variablen stark auf die Lehrernote wirkt. Die bisherigen Ergebnisse bestärken nämlich die Befürchtung, daß junge und alte Schüler verschiedenen Einflüssen unterworfen sind, die einander jedoch bei gleichzeitiger Betrachtung aller Schüler gegenseitig aufheben.
Überraschenderweise ist nur die Korrelation mit dem Anteil der Schüler mit Wiederholungsprüfung hoch signifikant (τ = 0,16), während die beiden anderen Variablen nicht signifikant mit der Lehrernote korrelieren (jeweils τ = 0,04).
Da sich also nur mehr eine unabhängige Variable anbietet, ist eine Regressionsanalyse nicht notwendig; das Bestimmtheitsmaß kann direkt durch Quadrierung des Korrelationskoeffizienten abgelesen werden. Allerdings ist zu beachten, daß es sich bei den obengenannten um Kendallsche Rangkorrelationskoeffizienten handelt, während in einer Regressionsanalyse mit der Maßkorrelation von Pearson gearbeitet wird. Zur Vergleichbarkeit der Resultate ist es daher sinnvoll, den Koeffizienten von Pearson zu betrachten: Dieser beträgt 0,20, das Bestimmtheitsmaß liegt also bei 0,04.
Zusammenfassend läßt sich also festhalten, daß sowohl bei den jüngeren als auch bei den älteren Schülern die betrachteten Variablen nur einen minimalen Teil der Varianz der Note für den Lehrer erklären, nämlich 12% bei den Unter-15jährigen und 4% bei den Ab-15jährigen. Dadurch ist meines Erachtens eindrucksvoll gezeigt, daß die eigene Note bei der Beurteilung des Lehrers für die Schüler keine wesentliche Rolle spielt; von „Rache“ kann also keineswegs die Rede sein.
„4) Wie oft hast Du schon eine Klasse wiederholt?“
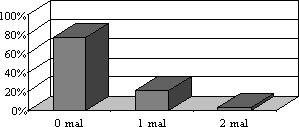

| Wert: | 0 mal | 1 mal | 2 mal | k.A. |
|---|---|---|---|---|
| Anzahl | 304 | 82 | 13 | 2 |
| Prozent i | 75,8 | 20,4 | 3,2 | 0,5 |
| Prozent g | 76,2 | 20,6 | 3,3 |
Die Repetentenquote ist mit nur knapp einem Viertel eigentlich relativ niedrig, wenn man bedenkt, daß vorwiegend leistungsschwache Schüler befragt wurden.
Eine Kreuztabelle zeigt zwar große Unterschiede zwischen jungen und alten Schülern, daraus zu schließen, daß Schüler ab 15 Jahren eher durchfallen als jüngere, wäre allerdings naiv, da die Differenzen wohl daher rühren, daß ältere Schüler einfach schon öfter „Gelegenheit“ zum Durchfallen hatten als jüngere.
Wesentlich interessanter ist ein Vergleich mit der Jahreszeugnisnote: So sind von den Schülern, die noch nie durchgefallen sind, „nur“ 80% im Zeugnis „negativ“, von denen, die schon mindestens einmal wiederholt haben, unglaubliche 95%. Dieser Unterschied ist laut einem U-Test hoch signifikant.
Dies legt den Schluß nahe, daß Schüler, die schon einmal durchgefallen sind, eher ein weiteres Mal versagen als Schüler, die noch nie eine Klasse wiederholt haben.
Zwischen den Geschlechtern und den Schularten bestehen nur geringe Abweichungen, die Mittelwerte differieren um weniger als 0,10.
„5) Wie oft davon warst Du auch in Mathematik negativ?“
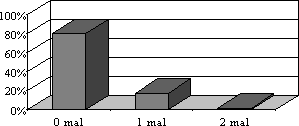

| Wert: | 0 mal | 1 mal | 2 mal | k.A. |
|---|---|---|---|---|
| Anzahl | 302 | 67 | 7 | 25 |
| Prozent i | 75,3 | 16,7 | 1,7 | 6,2 |
| Prozent g | 80,3 | 17,8 | 1,9 |
Das „Mitverschulden“ von Mathematik am Durchfallen scheint zwar auf den ersten Blick gering, es ist aber zu bedenken, daß gut drei Viertel der Befragten noch nie eine Klasse wiederholt haben. Eine gesonderte Betrachtung der „Durchfaller“ zeigt nämlich ein anderes Bild:
…wenn schon eine Klasse wiederholt
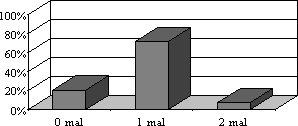
| Wert: | 0 mal | 1 mal | 2 mal | k.A. |
|---|---|---|---|---|
| Anzahl | 19 | 67 | 7 | 2 |
| Prozent i | 4,7 | 16,7 | 1,7 | 0,5 |
| Prozent g | 20,4 | 72 | 7,5 |
80% der Schüler, die schon (mindestens) einmal eine Klasse wiederholt haben, gaben an, (mindestens einmal) auch in Mathematik „negativ“ gewesen zu sein. Das zeigt sehr deutlich, daß Mathematik der Hauptgrund für vergangenes Versagen sein dürfte.
Gegen diesen Schluß kann zwar eingewendet werden, daß die Tatsache, daß jemand in Mathematik „negativ“ war, noch nicht heißt, daß Mathematik der Grund für sein Durchfallen war. So ist mir beispielsweise ein Schüler in Erinnerung, der zwar in fünf Gegenständen ein „Nicht genügend“ hatte, wovon jedoch nur einer das eigentliche „Problemfach“ war, während er in allen anderen einfach aufgegeben hat. Doch selbst solche (wahrscheinlich seltene) Fälle können wohl kaum eine 80%ige Beteiligung der Mathematik am Durchfallen erklären, wenn man an der Hypothese festhält, daß die Verteilung der „Problemfächer“ zufällig ist.
Konkret heißt das: Wenn ein Schüler, der in Mathematik leistungsschwach ist, schon einmal eine Klasse wiederholt hat, so ist die Wahrscheinlichkeit sehr hoch, daß er damals in Mathematik durchgefallen ist.
„6) In wie vielen Fächern hast Du eine Wiederholungsprüfung („Nachzipf“)?“
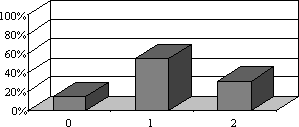

| Wert: | 0 | 1 | 2 | k.A. |
|---|---|---|---|---|
| Anzahl | 55 | 199 | 114 | 33 |
| Prozent i | 13,7 | 49,6 | 28,4 | 8,2 |
| Prozent g | 14,9 | 54,1 | 31 |
Wie erwartet hat mit 80% die überwiegende Mehrheit der befragten Schüler zumindest eine Wiederholungsprüfung. Überraschend sind hingegen jene 20%, die einen Lernkurs besuchen, obwohl sie keine Wiederholungsprüfung haben.
Ein Vergleich mit der Jahreszeugnisnote zeigt, daß von den Schülern mit Wiederholungsprüfung 90% im Zeugnis „negativ“ sind – also eine (bzw. die) Wiederholungsprüfung in Mathematik haben (das ist sicher, sofern keine falschen Angaben gemacht wurden). 3% sind im Zeugnis „positiv“ – haben also die Wiederholungsprüfung nicht in Mathematik – und 7% machten keine Angabe über die Zeugnisnote.
Von den Schülern mit einer Wiederholungsprüfung in Mathematik haben 37% außerdem noch eine Wiederholungsprüfung in einem anderen Fach. Die aus den Fragen 8 („Wie viele Schüler/innen in Deiner Klasse haben eine Wiederholungsprüfung in Mathematik (Dich eingerechnet)?“) und 9 („Wie viele Schüler/innen gehen in Deine Klasse (Dich eingerechnet)?“) errechnete durchschnittliche Quote an Wiederholungsprüfungen in Mathematik beträgt 18%. Es kann angenommen werden, daß Mathematik, was die Anzahl an Wiederholungsprüfungen betrifft, im Spitzenfeld des Fächerkanons liegt, da es in Mathematik die meisten „negativen“ Zeugnisnoten gibt (siehe Seite 9). Aufgrund der Stichprobenbeschaffenheit ist es außerdem so gut wie sicher, daß die tatsächliche Wiederholungsprüfungsquote unter dem errechneten Wert liegt, da Klassen ohne Wiederholungsprüfung wahrscheinlich unterrepräsentiert sind (siehe Seite 83). Aus diesen Annahmen kann geschlossen werden, daß sich die Wahrscheinlichkeit, daß ein Schüler eine Wiederholungsprüfung in einem anderen Fach hat, mindestens verdoppelt, wenn man weiß, daß er bereits in Mathematik einen „Nachzipf“ hat. Auf alle Fächer verallgemeinert hieße das, daß es wahrscheinlicher ist, daß ein Schüler mit einer Wiederholungsprüfung eine zweite hat, als daß ein anderer Schüler überhaupt eine hat. Dies würde das Stereotyp des schlechten Schülers (vgl. Höhn, 1980), der in mehreren Fächern versagt, bestätigen.
„7) Darfst Du in jedem Fall aufsteigen (mit „Klausel“)?“
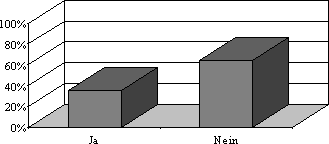

| Ja | Nein | k.A. | |
|---|---|---|---|
| Anzahl | 132 | 239 | 30 |
| Prozent i | 32,9 | 59,6 | 7,5 |
| Prozent g | 35,6 | 64,4 |
Die Mehrheit der Schüler darf nicht in jedem Fall aufsteigen; ein Vergleich mit der vorigen Frage 6 („In wie vielen Fächern hast Du eine Wiederholungsprüfung („Nachzipf“)?“) verstärkt diese Tendenz naturgemäß noch etwas: Von den Schülern mit Wiederholungsprüfung dürfen nur mehr knapp 30% sicher aufsteigen, bei 70% wird erst die Prüfung entscheiden. Diese Zahlen geben einen ungefähren Eindruck über die Praxis der Klauselvergabe.
Bei den Schülern mit Wiederholungsprüfung bestehen zwischen den Schularten so gut wie keine Unterschiede, bezüglich des Geschlechts zeigt eine Kreuztabelle zwar eine größere Abweichung (weibliche Schülerinnen haben die „Klausel“ öfter bekommen), diese ist laut einem U-Test jedoch nicht signifikant.
„8) Wie viele Schüler/innen in Deiner Klasse haben eine Wiederholungsprüfung in Mathematik (Dich eingerechnet)?“
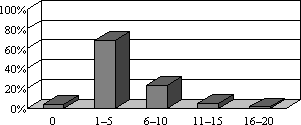
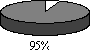
| Wert: | 0 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 | 6,5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 14 | 39 | 1 | 66 | 2 | 64 | 5 | 37 | 4 | 41 | 1 | 32 | 2 |
| Prozent i | 3,5 | 9,7 | 0,2 | 16,5 | 0,5 | 16 | 1,2 | 9,2 | 1 | 10,2 | 0,2 | 8 | 0,5 |
| Prozent g | 3,7 | 10,3 | 0,3 | 17,4 | 0,5 | 16,8 | 1,3 | 9,7 | 1,1 | 10,8 | 0,3 | 8,4 | 0,5 |
| Wert: | 7 | 7,5 | 8 | 8,5 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 17,5 | 20 | k.A. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 15 | 2 | 13 | 1 | 5 | 14 | 1 | 6 | 5 | 2 | 4 | 1 | 3 | 21 |
| Prozent i | 3,7 | 0,5 | 3,2 | 0,2 | 1,2 | 3,5 | 0,2 | 1,5 | 1,2 | 0,5 | 1 | 0,2 | 0,7 | 5,2 |
| Prozent g | 3,9 | 0,5 | 3,4 | 0,3 | 1,3 | 3,7 | 0,3 | 1,6 | 1,3 | 0,5 | 1,1 | 0,3 | 0,8 |
Eine Interpretation dieser Variable erscheint mir nur in Verbindung mit der Anzahl der Schüler in der Klasse zweckmäßig.
„9) Wie viele Schüler/innen gehen in Deine Klasse (Dich eingerechnet)?“
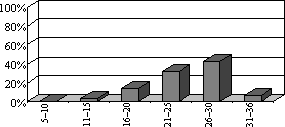

| Wert: | 5 | 7 | 8 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 1 | 1 | 1 | 1 | 1 | 3 | 1 | 6 | 9 | 8 |
| Prozent i | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,7 | 0,2 | 1,5 | 2,2 | 2 |
| Prozent g | 0,3 | 0,3 | 0,3 | 0,3 | 0,3 | 0,8 | 0,3 | 1,5 | 2,3 | 2 |
| Wert: | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 9 | 14 | 17 | 17 | 13 | 28 | 39 | 29 | 30 | 30 |
| Prozent i | 2,2 | 3,5 | 4,2 | 4,2 | 3,2 | 7 | 9,7 | 7,2 | 7,5 | 7,5 |
| Prozent g | 2,3 | 3,6 | 4,3 | 4,3 | 3,3 | 7,1 | 9,9 | 7,4 | 7,6 | 7,6 |
| Wert: | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | k.A. |
|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 41 | 46 | 20 | 11 | 5 | 2 | 4 | 4 | 2 | 8 |
| Prozent i | 10,2 | 11,5 | 5 | 2,7 | 1,2 | 0,5 | 1 | 1 | 0,5 | 2 |
| Prozent g | 10,4 | 11,7 | 5,1 | 2,8 | 1,3 | 0,5 | 1 | 1 | 0,5 |
Diese Ergebnisse sind besonders vorsichtig zu betrachten. Da wegen der Anonymität der Untersuchung nicht rekonstruiert werden kann, welche Fragebögen aus der selben Klasse stammen, muß davon ausgegangen werden, daß Mehrfachnennungen aus einer Klasse vorliegen. Da Mehrfachnennungen aus großen Klassen wahrscheinlicher sind als aus kleinen, dürften die errechneten Mittelwerte über den tatsächlichen liegen; sie können also lediglich als obere Grenze für die wahren Parameter interpretiert werden.
Die mittlere Klassenschülerzahl beträgt 24,9. Die AHS-Oberstufe unterscheiden sich mit Mittelwert 23,1 nur unwesentlich von den BHS mit 24,7. Deutlich ist hingegen die Differenz zwischen den Unter-15jährigen (26,4) und den Ab-15jährigen (23,8), sie beträgt 2,64. Die Anpassung an die Normalverteilung ist in diesen beiden Gruppen hinreichend, sodaß die Voraussetzung für einen t-Test gegeben ist. Dieser weist den Unterschied als höchst signifikant aus.
Anteil der Schüler mit Wiederholungsprüfung in Mathematik an der Klassenschülerzahl
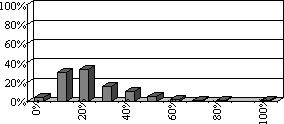
| Wert: | 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | 100% | k.A. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 13 | 101 | 111 | 53 | 35 | 17 | 5 | 3 | 2 | 0 | 2 | 59 |
| Prozent i | 3,2 | 25,2 | 27,7 | 13,2 | 8,7 | 4,2 | 1,2 | 0,7 | 0,5 | 0 | 0,5 | 14,7 |
| Prozent g | 3,8 | 29,5 | 32,5 | 15,5 | 10,2 | 5 | 1,5 | 0,9 | 0,6 | 0 | 0,6 |
Die Spaltenüberschriften sind jeweils die oberen Grenzen; in der Spalte „40%“ sind also beispielsweise alle Werte von über 30% bis 40% zusammengefaßt.
Die mittlere Quote liegt bei 18,8%, allerdings sind auch hier alle Durchschnittswerte aus den oben erläuterten Gründen mit großer Vorsicht zu behandeln.
In der AHS-Oberstufe beträgt der durchschnittliche Anteil 20,2%, in den BHS 27,2%; bei den Unter-15jährigen 13,5% und bei den Ab-15jährigen 22,6%.
Das an sich bei zwei Faktoren zur Signifikanzprüfung geeignete Verfahren der univariaten zweifaktoriellen Varianzanalyse ist hier problematisch, da es keine unter-15jährigen Schüler in BHS gibt, und daher eine der vier Zellen leer wäre. Außerdem ist die Anpassung der Werte an die Normalverteilung in allen vier Gruppen sehr mangelhaft, sodaß ich es für sinnvoller hielt, zwei U-Tests mit Korrektur der Irrtumswahrscheinlichkeit durchzuführen. Diese bewerteten den Unterschied zwischen jungen und alten Schülern als höchst signifikant, die Differenz zwischen AHS-Oberstufe und BHS jedoch als nicht signifikant.
„10) Wie hast Du im Mathematikunterricht aufgepaßt?“

| Wert: | 1 | 2 | 2,5 | 3 | 3,5 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 26 | 114 | 4 | 180 | 3 | 56 | 16 | 2 |
| Prozent i | 6,5 | 28,4 | 1 | 44,9 | 0,7 | 14 | 4 | 0,5 |
| Prozent g | 6,5 | 28,6 | 1 | 45,1 | 0,8 | 14 | 4 |
Ein Großteil der Schüler gibt an, mittelmäßig aufgepaßt zu haben; die Werte sind annähernd normalverteilt.
Kreuztabellen und Vergleiche der Mittelwerte zeigten weder zwischen den Geschlechtern, noch nach Schulart, Alter oder „positiver“ bzw. „negativer“ Jahreszeugnisnote deutliche Unterschiede; die Abweichungen der Mittelwerte lagen stets unter 0,30. Eine weiterführende Analyse der Differenzen zwischen diesen Gruppen hielt ich daher nicht für gerechtfertigt.
Aufgrund der hohen Abhängigkeit der Jahreszeugnisnote von den Schularbeiten hat mich natürlich die Frage interessiert, inwieweit das Aufpassen im Unterricht die Note beeinflußt. Dabei zeigte sich tatsächlich eine erstaunlich niedrige Rangkorrelation von nur 0,10. Das Bestimmtheitsmaß beträgt daher 0,01, was bedeutet, daß nur 1% der Varianz der Jahreszeugnisnote durch das Aufpassen im Unterricht erklärt wird. Bei Verwendung des Koeffizienten von Pearson erhöht sich die Korrelation zwar leicht auf 0,12, das Bestimmtheitsmaß bleibt aber bei 0,01.
Die Aufmerksamkeit im Unterricht scheint also keinen Einfluß auf die Note zu haben, und zwar weder über die Beurteilung der Mitarbeit noch aufgrund des (zu erwartenden) größeren Wissens bei höherer Aufmerksamkeit.
Auch mit der Note für den Mathematiklehrer besteht nur eine geringe Korrelation: 0,11 nach Kendall und 0,13 nach Pearson. Ob ein Schüler aufpaßt oder nicht, dürfte also nicht davon abhängen, ob er mit seinem Lehrer zufrieden ist, bzw. hängt die Zufriedenheit mit dem Lehrer nicht vom Aufpassen ab.
„11) Wie oft habt Ihr in Mathematik eine Hausübung bekommen?“

| Wert: | 1 | 1,5 | 2 | 3 | 3,5 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 236 | 2 | 105 | 21 | 1 | 25 | 8 | 3 |
| Prozent i | 58,9 | 0,5 | 26,2 | 5,2 | 0,2 | 6,2 | 2 | 0,7 |
| Prozent g | 59,3 | 0,5 | 26,4 | 5,3 | 0,3 | 6,3 | 2 |
Die Mehrheit der Schüler gibt an, immer (oder zumindest meistens) eine Hausübung bekommen zu haben, 86% geben den Wert 1 oder 2.
Überraschenderweise gibt es kaum Unterschiede zwischen jungen und alten Schülern, die Mittelwerte unterscheiden sich nur um 0,14. In der Oberstufe dürfte also genauso oft eine Hausübung gegeben werden wie in der Unterstufe.
Ganz anders zeigt sich hingegen die Situation bei Vergleich der Schularten: Während der Mittelwert in den BHS bei nur 2,25 liegt, klettert er in der AHS-Oberstufe auf 1,50; die Differenz beträgt 0,75. Dieser Unterschied ist laut einem U-Test höchst signifikant.
Matschinger kam bei ihrer Untersuchung an 277 Schülern der AHS-Unterstufe zu folgendem Ergebnis: 59% gaben an, jede Stunde eine Mathematikhausübung zu bekommen, 41% fast jede Stunde (vgl. Matschinger, 1994, S. 72). Bei Einschränkung auf die 155 AHS-Unterstufenschüler der vorliegenden Erhebung stimmen die Ergebnisse damit im großen und ganzen überein: 66,5% gaben den Wert 1, 25,2% den Wert 2, zusammen also 91,6% den Wert 1 oder 2, was sich mit der Angabe „jede Mathematikstunde“ oder „fast jede Mathematikstunde“ bei Matschinger ungefähr deckt.
„12) Wie oft hast Du die Hausübung (selbst!) gemacht?“

| Wert: | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 43 | 1 | 112 | 1 | 114 | 3 | 92 | 32 | 3 |
| Prozent i | 10,7 | 0,2 | 27,9 | 0,2 | 28,4 | 0,7 | 22,9 | 8 | 0,7 |
| Prozent g | 10,8 | 0,3 | 28,1 | 0,3 | 28,6 | 0,8 | 23,1 | 8 |
Die Hausübungs-Moral ist eher schlecht, nur knapp 30% geben den Wert 1 oder 2, machen die Hauübung also immer oder zumindest meistens; ungefähr ebenso viele Schüler machen die Hausübung nie oder fast nie.
Die Verteilung zeigt auf den ersten Blick ein ähnliches Bild wie bei Frage 10 („Wie hast Du im Mathematikunterricht aufgepaßt?“). Da man geneigt ist anzunehmen, daß jene Schüler, die im Unterricht aufpassen, eher die Hausübung machen, würde man also eine hohe Korrelation erwarten. Tatsächlich ist die Maßkorrelation mit 0,29 jedoch gering; es dürfte also doch kein allzu großer Zusammenhang zwischen Aufpassen und Hausübung Machen bestehen.
Kreuztabellen und Mittelwertvergleiche zeigen deutliche Unterschiede zwischen Schülern mit „positiver“ und „negativer“ Jahreszeugnisnote und nach dem Alter. Der Mittelwert bei den Ab-15jährigen liegt mit 3,27 sogar um 0,92 über jenem der Unter-15jährigen (2,35)!
Fast identisch ist hingegen die Verteilung in beiden Geschlechtern, die Mittelwerte differieren nur um 0,07; der Unterschied zwischen den Schularten ist auch nur kaum stärker.
Um die Abweichungen nach der Zeugnisnote und dem Alter auf Signifikanz zu prüfen, wollte ich eine univariate zweifaktorielle Varianzanalyse durchführen, allerdings sind die Voraussetzungen nur teilweise erfüllt: Die Anpassung an die Normalverteilung ist zwar in allen vier Gruppen gut, jedoch sind die Unterschiede der Varianzen sowohl laut dem Test von Cochran, als auch von Bartlett & Box signifikant. Ich habe dennoch eine Varianzanalyse gerechnet, diese jedoch durch zwei t-Tests mit Korrektur der Irrtumswahrscheinlichkeit ergänzt.
Die Varianzanalyse weist die Unterschiede zwischen den Zellen als höchst signifikant aus. Von den Haupteffekten ist das Alter höchst signifikant, die Jahreszeugnisnote hingegen nicht signifikant, allerdings bestehen auch eine signifikante Wechselwirkung zwischen den beiden Faktoren, was die Signifikanzprüfung der Haupteffekte etwas in Frage stellt.
Etwas anders das Ergebnis der beiden t-Tests: Hier ist auch nach Anpassung der Irrtumswahrscheinlichkeit der Unterschied zwischen Schülern mit „positiver“ und solchen mit „negativer“ Jahreszeugnisnote signifikant. Die Differenz zwischen den beiden Altersgruppen ist nach wie vor höchst signifikant.
„13) Wenn Du die Hausübung nicht (selbst) gemacht hast, warum nicht?“
„Sie war mir zu schwer“
| Wert: | 1 | 1,5 | 2 | 2,5 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 128 | 1 | 82 | 3 | 90 | 36 | 46 | 15 |
| Prozent i | 31,9 | 0,2 | 20,4 | 0,7 | 22,4 | 9 | 11,5 | 3,7 |
| Prozent g | 33,2 | 0,3 | 21,2 | 0,8 | 23,3 | 9,3 | 11,9 |
„Sie erschien mir sinnlos“

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 40 | 40 | 46 | 52 | 207 | 16 |
| Prozent i | 10 | 10 | 11,5 | 13 | 51,6 | 4 |
| Prozent g | 10,4 | 10,4 | 11,9 | 13,5 | 53,8 |
„Sie wurde nicht kontrolliert“

| Wert: | 1 | 2 | 3 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 47 | 36 | 23 | 34 | 2 | 245 | 14 |
| Prozent i | 11,7 | 9 | 5,7 | 8,5 | 0,5 | 61,1 | 3,5 |
| Prozent g | 12,1 | 9,3 | 5,9 | 8,8 | 0,5 | 63,3 |
„Sie hatte keinen Einfluß auf die Note“

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 32 | 18 | 33 | 38 | 265 | 15 |
| Prozent i | 8 | 4,5 | 8,2 | 9,5 | 66,1 | 3,7 |
| Prozent g | 8,3 | 4,7 | 8,5 | 9,8 | 68,7 |
„Ich habe keine Zeit gehabt“

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 65 | 58 | 75 | 63 | 125 | 15 |
| Prozent i | 16,2 | 14,5 | 18,7 | 15,7 | 31,2 | 3,7 |
| Prozent g | 16,8 | 15 | 19,4 | 16,3 | 32,4 |
„anderer Grund“
| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 64 | 20 | 24 | 7 | 121 | 165 |
| Prozent i | 16 | 5 | 6 | 1,7 | 30,2 | 41,1 |
| Prozent g | 27,1 | 8,5 | 10,2 | 3 | 51,3 |
„welcher?“
| Grund: | keine Lust |
faul |
vergessen |
kein Interesse |
persönliche Probleme |
Freunde |
Hobby |
nicht ausgekannt |
abgeschrieben |
aufgegeben |
krank |
Freizeit |
keine Motivation |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 38 | 30 | 8 | 6 | 6 | 5 | 4 | 4 | 3 | 3 | 3 | 2 | 2 |
| Prozent i | 9,5 | 7,5 | 2 | 1,5 | 1,5 | 1,2 | 1 | 1 | 0,7 | 0,7 | 0,7 | 0,5 | 0,5 |
| Prozent g | 30,4 | 24 | 6,4 | 4,8 | 4,8 | 4 | 3,2 | 3,2 | 2,4 | 2,4 | 2,4 | 1,6 | 1,6 |
| Grund: | zu viel andere Hausübungen |
Angst |
bin ein Träumer |
pure Fadess |
ich hasse Hausübung |
keine Konzentration |
machte keiner |
unklar, welche Hausübung |
vergessen, was Hausübung war |
war mir egal |
zu viel |
k.A. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 276 |
| Prozent i | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 68,8 |
| Prozent g | 0,8 | 0,8 | 0,8 | 0,8 | 0,8 | 0,8 | 0,8 | 0,8 | 0,8 | 0,8 | 0,8 |
Ein klarer Grund für das Nichtmachen der Hausübung ist nicht erkennbar, dafür drei Faktoren, an denen es eindeutig nicht liegt. Jeweils eine große Mehrheit der Schüler gibt an, daß ihnen die Hausübung nicht sinnlos erschienen ist und daß auch nicht die mangelnde Kontrolle oder der geringe Einfluß auf die Note der Grund war, wenn sie die Hausübung nicht gemacht haben.
Bei Umkehr dieser Schlüsse ergibt sich, daß die meisten Befragten der Meinung sind, daß ihre Hausübungen sinnvoll sind, diese auch kontrolliert und entsprechend bei der Benotung mitberücksichtigt werden. Diese Schlußweise ist allerdings problematisch, da aufgrund der Fragestellung nicht explizit auf die Umkehrung geschlossen werden kann. Vor allem muß bezweifelt werden, daß die Hausübungen tatsächlich einen ernst zu nehmenden Einfluß auf die Zeugnisnote ausüben, da die Regressionsanalyse bei Frage 1 ergeben hat, daß drei Viertel der Varianz der Jahreszeugnisnote nur durch die Schularbeiten erklärt wird. Da das verbleibende Viertel wohl auch von einigen anderen Faktoren (wie z. B. Mitarbeit, mündliche Prüfungen, persönlicher Eindruck) determiniert wird, dürfte der Einfluß der Hausübungen gering bleiben.
Bezüglich der Sinnhaftigkeit und der Kontrolle der Hausübung wird die Umkehrung des Schlusses allerdings durch die Ergebnisse von Matschinger zumindest bezüglich der AHS-Unterstufe gestützt: So gaben bei ihr auf die Frage „Glaubst Du, daß Dir die Mathematikhausübungen helfen, den Unterrichtsstoff besser zu verstehen?“ 52%, auf die Frage „Es wird kontrolliert, ob alle die HÜ haben“ 53% die Antwort „immer“ oder „meistens“ (vgl. Matschinger, 1994, S. 90 und S. 110).
Wenngleich sich kein eindeutiger Grund abzeichnet, warum die Hausaufgaben nicht erledigt werden, so sind doch zwei Ursachen einigermaßen gut erkennbar: die Schwierigkeit der Hausübung und die Faulheit der Schüler. Faßt man nämlich die beiden von den Befragten selbst angegebenen Gründe „keine Lust“ und „faul“ zusammen, so kommen sie auf beachtliche 68 spontane Nennungen, das sind 17%.
Bei der Variable „Sie war mir zu schwer“ zeigt sich bei näherer Betrachtung ein interessanter Effekt: Während sich nämlich weder die beiden Schularten, noch die beiden Altersgruppen, oder Schüler mit „positiver“ von solchen mit „negativer“ Jahreszeugnisnote erkennbar unterscheiden, liegt der Mittelwert der weiblichen Schülerinnen um beachtliche 0,61 unter dem der männlichen (2,15 gegenüber 2,76). Die Signifikanz dieser Abweichung ist schon mit freiem Auge erkennbar, eine exakte Prüfung habe ich aber dennoch unterlassen. Ich sehe nämlich keinen Grund zur Annahme, daß weiblichen Schülerinnen die Hausübung tatsächlich öfter zu schwierig ist als männlichen, sondern glaube viel eher, daß Mädchen stärker bereit sind, das auch zuzugeben. Männliche Schüler dürften also lediglich andere Gründe vorschieben; bei den selbst genannten Ursachen „keine Lust“ und „faul“ konnte ich jedoch keinen Geschlechtsunterschied feststellen.
Ganz ähnliche Ergebnisse erzielte Matschinger bei ihrer Erhebung an AHS-Unterstufenschülern: Bei der Frage „Weißt Du, wie Du die Beispiele lösen mußt?“ ergaben sich höchst signifikante Unterschiede zwischen Mädchen und Buben. Matschinger zieht daraus den Schluß, „daß Burschen wesentlich häufiger wissen, wie die Beispiele zu lösen sind, als Mädchen.“ (Matschinger, 1994, S. 84). Dieser Schlußfolgerung kann ich mich wie gesagt nicht anschließen.
Unter den fünf vorgegebenen Variablen bestehen nur geringe Zusammenhänge. Einzig zwischen „Sie wurde nicht kontrolliert“ und „Sie hatte keinen Einfluß auf die Note“ beträgt der Maßkorrelationskoeffizient 0,48 und ist höchst signifikant; alle anderen Koeffizienten liegen unter 0,22.
Eine Trennung nach den Vergleichskategorien Alter, Geschlecht, Schulart und Jahreszeugnisnote ergab bei den Variablen „Sie erschien mir sinnlos“ und „Sie hatte keinen Einfluß auf die Note“ keine auffallenden Unterschiede.
Abweichungen zeigten hingegen die Variablen „Sie wurde nicht kontrolliert“ und „Ich habe keine Zeit gehabt“: Bei ersterer bestehen Unterschiede bei Trennung nach Schulart, Alter und Jahreszeugnisnote, bei letzter nach Geschlecht, Alter und Zeugnisnote; die jeweiligen Mittelwerte weichen zwischen 0,31 und 0,39 voneinander ab.
Eine multivariate mehrfaktorielle Varianzanalyse scheint mir hier zur Signifikanzprüfung nicht angebracht, da einerseits die beiden abhängigen Variablen nur schwach korrelieren und andererseits jeweils andere Faktoren zu testen sind.
Da bei der Variable „Sie wurde nicht kontrolliert“ gleichzeitig der Einfluß von Alter und Schulart zu untersuchen ist, ist auch eine univariate Varianzanalyse ungeeignet, da es keine unter-15jährigen Schüler in BHS gibt und daher zwei der acht Zellen leer wären.
Aufgrund der schlechten Anpassung der Werte an die Normalverteilung habe ich drei U-Tests mit korrigierter Irrtumswahrscheinlichkeit gerechnet, diese brachten jedoch alle kein signifikantes Ergebnis.
Zum Test der anderen Differenzen habe ich eine univariate mehrfaktorielle Varianzanalyse mit „Ich habe keine Zeit gehabt“ als abhängiger Variable und dem Geschlecht, dem Alter und der Zeugnisnote als Faktoren durchgeführt.
Die Anpassung der Werte an die Normalverteilung ist in allen sechs Gruppen schlecht, die Varianzen sind jedoch sowohl nach dem Test von Cochran als auch von Bartlett & Box homogen. Aufgrund dieser teilweisen Verletzung der Voraussetzungen habe ich zusätzlich drei U-Tests mit Korrektur der Irrtumswahrscheinlichkeit vorgenommen.
Die Varianzanalyse ist nur knapp signifikant, die Wechselwirkungen sind ebenso wie die Faktoren Zeugnisnote und Geschlecht nicht signifikant; die beiden U-Tests bringen hier das selbe Ergebnis. Einzig die Unterschiede zwischen den Altersgruppen erweisen sich beim U-Test als signifikant, bei der Varianzanalyse sogar als hoch signifikant.
Zusammenfassend läßt sich also festhalten, daß als Gründe für das Nichtmachen der Hausübung am ehesten die Schwierigkeit und die Faulheit der Schüler zu nennen sind, alle anderen vorgegebenen Ursachen können eindeutig abgelehnt werden. Alle Vergleichsgruppen antworten ähnlich, lediglich beim Eingestehen der Schwierigkeit der Hausübung sind die weiblichen Schülerinnen den männlichen weit voraus. Darüber hinaus geben ältere Schüler etwas öfter „keine Zeit“ als Grund an als jüngere.
„14) Was hältst Du davon, wenn nicht alle Schüler/innen die selbe Hausübung bekommen, sondern eine an ihr Können angepaßte?“

| Wert: | 1 | 1,5 | 2 | 2,5 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 103 | 1 | 73 | 1 | 77 | 35 | 103 | 8 |
| Prozent i | 25,7 | 0,2 | 18,2 | 0,2 | 19,2 | 8,7 | 25,7 | 2 |
| Prozent g | 26,2 | 0,3 | 18,6 | 0,3 | 19,6 | 8,9 | 26,2 |
Diese in der letzten Zeit oft erhobene Forderung (vgl. beispielsweise Matschinger, 1994, S. 127) findet bei den Schülern selbst überraschend wenig Anklang, der Mittelwert liegt bei 2,90. An sich wäre ja zu erwarten, daß gerade besonders Leistungsstarke und Leistungsschwache von einer Differenzierung der Hausübungen profitieren; eine indifferente Haltung würde man demnach am ehesten bei Schülern der mittleren Leistungsstärke vermuten.
Bei einer Untersuchung von Scharf an einer Grazer HAK 1988 gaben zwar 42% der befragten 26 Lehrer an, differenzierte Hausübungen zu stellen (vgl. Scharf, 1988, S. 74), aufgrund der Fragestellung („Nehmen Sie Rücksicht auf schwächere Schüler, indem Sie differenzierte Hausübungen geben? - ja / nein“) muß jedoch bezweifelt werden, daß tatsächlich ein so großer Teil der Lehrer von dieser Möglichkeit Gebrauch macht.
Überraschend sind die niedrigen Korrelationen zu den Antworten „Sie war mir zu schwer“ und „Sie erschien mir sinnlos“ der vorigen Frage 13 („Wenn Du die Hausübung nicht (selbst) gemacht hast, warum nicht?“); beide Koeffizienten liegen unter 0,09. Die Akzeptanz von verschiedenen Hausübungen steigt also nicht mit dem Eindruck, daß die Hausübungen zu schwierig oder sinnlos sind.
Bei getrennter Betrachtung nach Geschlecht, Alter, Jahreszeugnisnote und Schulart zeigten sich keine nennenswerten Unterschiede, die Mittelwerte unterscheiden sich stets um weniger als 0,23. Etwas überraschend ist die Tatsache, daß differenzierte Hausübungen auch bei älteren Schülern nicht beliebter sind als bei jüngeren.
„15) Wann hast Du im abgelaufenen Schuljahr Mathematik gelernt?“
„regelmäßig“
| Wert: | 1 | 2 | 2,5 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 23 | 31 | 1 | 81 | 81 | 168 | 16 |
| Prozent i | 5,7 | 7,7 | 0,2 | 20,2 | 20,2 | 41,9 | 4 |
| Prozent g | 6 | 8,1 | 0,3 | 21 | 21 | 43,6 |
„vor Schularbeiten“

| Wert: | 1 | 2 | 2,5 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 192 | 97 | 2 | 58 | 20 | 30 | 2 |
| Prozent i | 47,9 | 24,2 | 0,5 | 14,5 | 5 | 7,5 | 0,5 |
| Prozent g | 48,1 | 24,3 | 0,5 | 14,5 | 5 | 7,5 |
„am Ende des ersten Semesters“

| Wert: | 1 | 2 | 3 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 56 | 46 | 79 | 60 | 1 | 155 | 4 |
| Prozent i | 14 | 11,5 | 19,7 | 15 | 0,2 | 38,7 | 1 |
| Prozent g | 14,1 | 11,6 | 19,9 | 15,1 | 0,3 | 39 |
„am Ende des zweiten Semesters“

| Wert: | 1 | 2 | 3 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 142 | 49 | 61 | 41 | 1 | 105 | 2 |
| Prozent i | 35,4 | 12,2 | 15,2 | 10,2 | 0,2 | 26,2 | 0,5 |
| Prozent g | 35,6 | 12,3 | 15,3 | 10,3 | 0,3 | 26,3 |
„wann anders“
| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 22 | 10 | 20 | 10 | 151 | 188 |
| Prozent i | 5,5 | 2,5 | 5 | 2,5 | 37,7 | 46,9 |
| Prozent g | 10,3 | 4,7 | 9,4 | 4,7 | 70,9 |
„wann?“
| Zeit: | Ferien |
bei Gelegenheit |
Prüfungen |
Tests |
Wiederholungen |
Beginn 2. Semester |
Entscheidungsprüfung |
Prüfung |
Schulanfang |
bei Lust |
bis 4. Schularbeit |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 11 | 11 | 5 | 3 | 3 | 2 | 2 | 2 | 2 | 1 | 1 |
| Prozent i | 2,7 | 2,7 | 1,2 | 0,7 | 0,7 | 0,5 | 0,5 | 0,5 | 0,5 | 0,2 | 0,2 |
| Prozent g | 20,8 | 20,8 | 9,4 | 5,7 | 5,7 | 3,8 | 3,8 | 3,8 | 3,8 | 1,9 | 1,9 |
| Zeit: | immer |
mündliche Wiederholungen |
Mitte 2. Semester |
Pfingsten |
Stunde vor Schularbeit |
täglich |
wenn gezwungen |
wenn nicht ausgekannt |
wenn nötig |
Zwischenprüfungen |
k.A. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 348 |
| Prozent i | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 86,8 |
| Prozent g | 1,9 | 1,9 | 1,9 | 1,9 | 1,9 | 1,9 | 1,9 | 1,9 | 1,9 | 1,9 |
Erwartungsgemäß lernen die Schüler vor allem dann, wenn es darauf ankommt, nämlich vor Schularbeiten und am Ende des Schuljahres; jeweils knapp drei Viertel (72,1%) bzw. knapp die Hälfte (47,6%) geben den Wert 1 oder 2. Regelmäßig wird kaum gelernt, knapp zwei Drittel (62,1%) antworten mit dem Wert 4 oder 5. Am Ende des ersten Semesters lernen einige viel und einige wenig; die Gründe dafür könnten sein, daß das Semesterzeugnis von vielen nicht so wichtig genommen wird wie das Jahreszeugnis, oder daß aufgrund der allgemein besseren Noten auf die ersten drei Schularbeit der Lernbedarf nicht so groß ist.
Die einzige hohe Korrelation zwischen den vier vorgegebenen Variablen besteht mit 0,45 zwischen „am Ende des ersten Semesters“ und „am Ende des zweiten Semesters“; dieser Zusammenhang ist höchst signifikant. Alle anderen Maßkorrelationskoeffizienten liegen unter 0,25.
Eine getrennte Betrachtung nach der Jahreszeugnisnote zeigt teilweise große Unterschiede bei den Variablen „am Ende des ersten Semesters“, „am Ende des zweiten Semesters“ und „regelmäßig“. Bei letzterer weichen auch die Altersgruppen stark voneinander ab; sonst bestehen kaum Abweichungen zwischen den Vergleichsgruppen.
Da die beiden Semesterende-Variablen deutlich miteinander korrelieren, habe ich die Prüfung der Unterschiede nach der Zeugnisnote durch eine multivariate einfaktorielle Varianzanalyse vorgenommen.
Die Voraussetzungen sind leider nur mangelhaft erfüllt: Die Anpassung
der Werte an die Normalverteilung ist in beiden Gruppen in beiden Variablen
schlecht und der multivariate Test von Box ergibt signifikante Unterschiede
zwischen den Varianzen, die univariaten Tests von Cochran und Bartlett &
Box kommen jedoch in beiden Variablen zu keinem signifikanten Ergebnis.
Da es aber kein anderes geeignetes Verfahren zur Messung von Unterschieden in
korrelierten Variablen gibt, habe ich die Varianzanalyse dennoch durchgeführt.
Alle drei multivariaten Tests von Pillai, Wilks und Hotelling zeigen hoch signifikante Differenzen zwischen den Zellen, univariate Tests berechnen den Unterschied in der Variable „am Ende des ersten Semesters“ als knapp signifikant, in der Variable „am Ende des zweiten Semesters“ hingegen als hoch signifikant. Die Abweichungen gehen in die Richtung, daß Schüler mit „negativer“ Note am Ende beider Semester mehr lernen als solche, die im Zeugnis „positiv“ sind; die Mittelwerte für das erste Semester differieren um 0,40 (3,50 bzw. 3,90), jene für das zweite Semester sogar um 0,69 (2,71 bzw. 3,40).
Zur Untersuchung der Unterschiede nach Zeugnisnote und Alter bei der Variable „regelmäßig“ habe ich eine univariate mehrfaktorielle Varianzanalyse gerechnet.
Auch hier sind die Voraussetzungen leider nur teilweise erfüllt: Die Tendenz zur Normalverteilung ist zwar in allen vier Zellen schlecht, die Varianzen sind jedoch nach den Tests von Cochran und Bartlett & Box homogen. Da im univariaten Fall die Möglichkeit besteht, auf U-Tests mit korrigierter Irrtumswahrscheinlichkeit auszuweichen, habe ich diese angeschlossen.
Die Varianzanalyse ist insgesamt signifikant, der Einfluß der Wechselwirkungen und der Zeugnisnote ist jedoch nicht signifikant. Die beiden Altersgruppen unterscheiden sich dagegen höchst signifikant, und zwar liegt der Mittelwert der Unter-15jährigen mit 3,51 um 0,63 über jenem der Ab-15jährigen (4,13).
Die U-Tests bestätigen die Varianzanalyse völlig, indem sie nach dem Alter ein höchst signifikantes, nach der Zeugnisnote aufgrund der Korrektur der Irrtumswahrscheinlichkeit jedoch ein nicht signifikantes Ergebnis hervorbringen.
Zusammenfassend kann man sagen, daß der Großteil der Schüler hauptsächlich vor Schularbeiten und am Jahresende lernt, bei detaillierter Betrachtung zeigen sich jedoch interessante Zusammenhänge: Während Schüler mit „negativer“ Jahreszeugnisnote am Ende jedes Semesters signifikant mehr lernen als ihre Kollegen mit „positiver“ Note, studieren diese regelmäßig mehr; diese Abweichung ist jedoch nicht signifikant, die Mittelwerte liegen um 0,35 auseinander (3,95 bzw. 3,60). Regelmäßiges Mitlernen könnte also eine Art Erfolgsrezept für die „positive“ Note sein.
Die beiden Altersgruppen unterscheiden sich nur bezüglich des regelmäßigen Lernens höchst signifikant, Unter-15jährige sind deutlich stärker zur konstanten Arbeit mit der Mathematik bereit. In dieser Altersgruppe fand auch Matschinger einen starken Trend zur Regelmäßigkeit: 19% der befragten AHS-Unterstufenschüler gaben an, immer mitzulernen, 56% lernen mit und vor der Schularbeit noch intensiver (vgl. Matschinger, 1994, S. 93 und S. 169, Frage 19).
„16) Welche Ursachen machst Du für Deine schlechten Leistungen in Mathematik verantwortlich?“
„fehlendes Grundwissen“

| Wert: | 1 | 2 | 3 | 3,5 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 62 | 61 | 97 | 1 | 60 | 1 | 113 | 6 |
| Prozent i | 15,5 | 15,2 | 24,2 | 0,2 | 15 | 0,2 | 28,2 | 1,5 |
| Prozent g | 15,7 | 15,4 | 24,6 | 0,3 | 15,2 | 0,3 | 28,6 |
„falsch gelernt“
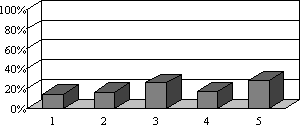

| Wert: | 1 | 2 | 3 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 56 | 64 | 100 | 67 | 1 | 109 | 4 |
| Prozent i | 14 | 16 | 24,9 | 16,7 | 0,2 | 27,2 | 1 |
| Prozent g | 14,1 | 16,1 | 25,2 | 16,9 | 0,3 | 27,5 |
„zu wenig gelernt“
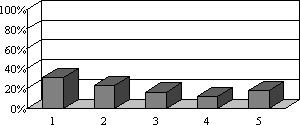

| Wert: | 1 | 1,5 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 123 | 1 | 90 | 64 | 47 | 71 | 5 |
| Prozent i | 30,7 | 0,2 | 22,4 | 16 | 11,7 | 17,7 | 1,2 |
| Prozent g | 31,1 | 0,3 | 22,7 | 16,2 | 11,9 | 17,9 |
„zu wenig / keine Nachhilfe“
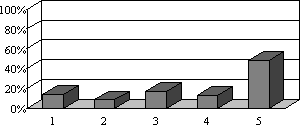

| Wert: | 1 | 2 | 3 | 3,5 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 53 | 32 | 66 | 1 | 49 | 1 | 188 | 11 |
| Prozent i | 13,2 | 8 | 16,5 | 0,2 | 12,2 | 0,2 | 46,9 | 2,7 |
| Prozent g | 13,6 | 8,2 | 16,9 | 0,3 | 12,6 | 0,3 | 48,2 |
„sinnlose Hausübungen“
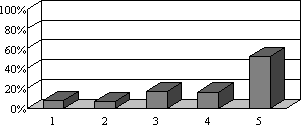

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 30 | 28 | 67 | 64 | 205 | 7 |
| Prozent i | 7,5 | 7 | 16,7 | 16 | 51,1 | 1,7 |
| Prozent g | 7,6 | 7,1 | 17 | 16,2 | 52 |
„zu wenig Hausübungen gemacht“

| Wert: | 1 | 1,5 | 2 | 3 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 112 | 1 | 66 | 56 | 47 | 1 | 113 | 5 |
| Prozent i | 27,9 | 0,2 | 16,5 | 14 | 11,7 | 0,2 | 28,2 | 1,2 |
| Prozent g | 28,3 | 0,3 | 16,7 | 14,1 | 11,9 | 0,3 | 28,5 |
„mangelnde Begabung“

| Wert: | 1 | 1,5 | 2 | 3 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 67 | 1 | 40 | 96 | 55 | 3 | 133 | 6 |
| Prozent i | 16,7 | 0,2 | 10 | 23,9 | 13,7 | 0,7 | 33,2 | 1,5 |
| Prozent g | 17 | 0,3 | 10,1 | 24,3 | 13,9 | 0,8 | 33,7 |
„Mathematiklehrer/in“

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 123 | 69 | 66 | 37 | 95 | 11 |
| Prozent i | 30,7 | 17,2 | 16,5 | 9,2 | 23,7 | 2,7 |
| Prozent g | 31,5 | 17,7 | 16,9 | 9,5 | 24,4 |
„Schulangst, Prüfungsangst“

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 102 | 71 | 75 | 49 | 101 | 3 |
| Prozent i | 25,4 | 17,7 | 18,7 | 12,2 | 25,2 | 0,7 |
| Prozent g | 25,6 | 17,8 | 18,8 | 12,3 | 25,4 |
„persönliche (z.B. familiäre) Gründe“

| Wert: | 1 | 2 | 3 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 40 | 20 | 34 | 39 | 2 | 254 | 12 |
| Prozent i | 10 | 5 | 8,5 | 9,7 | 0,5 | 63,3 | 3 |
| Prozent g | 10,3 | 5,1 | 8,7 | 10 | 0,5 | 65,3 |
„etwas anderes“
| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 30 | 4 | 9 | 1 | 164 | 193 |
| Prozent i | 7,5 | 1 | 2,2 | 0,2 | 40,9 | 48,1 |
| Prozent g | 14,4 | 1,9 | 4,3 | 0,5 | 78,8 |
„was?“
| Ursache: | faul |
kein Interesse |
keine Lust |
Freund(e) |
gefehlt |
andere Fächer |
keine Zeit |
Konzentration |
Laune |
nicht aufgepaßt |
Angst |
Freizeit |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 11 | 7 | 4 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 1 | 1 |
| Prozent i | 2,7 | 1,7 | 1 | 0,7 | 0,7 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,2 | 0,2 |
| Prozent g | 22 | 14 | 8 | 6 | 6 | 4 | 4 | 4 | 4 | 4 | 2 | 2 |
| Ursache: | dummeFehler |
Fernsehen |
Schularbeiten |
Müdigkeit |
Nervosität |
Pech |
Schülervertretung |
Schulwechsel |
Schwester |
zulangsam |
k.A. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 351 |
| Prozent i | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 87,5 |
| Prozent g | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
Auf den ersten Blick lassen sich zwar keine einheitlichen Gründe für die schlechten Leistungen erkennen, es haben jedoch 323 Schüler (81%) bei mindestens einer Variable den Wert 1 gegeben. Es liegt also nahe, die Anzahl der relevanten Variablen mittels einer Faktorenanalyse zu reduzieren.
Die Eignung der Daten für die Analyse ist zufriedenstellend: Der Bartlett-Test auf Sphärizität ergibt, daß sich die betrachteten Korrelationen höchst signifikant von null unterscheiden, und die Prüfgröße von Kaiser, Meyer & Olkin beträgt 0,65. Durch Betrachtung der Eigenwerte habe ich mich für drei Faktoren entschieden, diese erklären insgesamt 48% der Gesamtvarianz. Nach der Rotation ergab sich folgende Faktorladungsmatrix (Korrelationen unter 0,30 habe ich weggelassen):
| Variable: | Faktor 1 | Faktor 2 | Faktor 3 |
|---|---|---|---|
| zu wenig gelernt | 0,83 | ||
| zu wenig Hausübungen gemacht | 0,72 | ||
| zu wenig / keine Nachhilfe | 0,50 | 0,32 | |
| fehlendes Grundwissen | 0,65 | ||
| Schulangst, Prüfungsangst | –0,48 | 0,58 | |
| falsch gelernt | 0,57 | ||
| mangelnde Begabung | 0,48 | ||
| persönliche (z.B. familiäre) Gründe | 0,42 | ||
| Mathematiklehrer/in | 0,77 | ||
| sinnlose Hausübungen | 0,77 |
Im ersten Faktor sind jene Gründe zusammengefaßt, die beim Schüler selbst liegen, nämlich „zu wenig gelernt“, „zu wenig Hausübungen gemacht“ und „zu wenig / keine Nachhilfe“. Diese Gründe gehen außerdem mit wenig Angst einher, was auch nicht verwundert, da jene Schüler, die wenig lernen, meist auch keine Angst vor Prüfungen haben, da sie ja sonst mehr gelernt hätten. Als Bezeichnung für diesen Faktor bietet sich „Selbst“ an.
Der zweite Faktor wird von den Variablen „fehlendes Grundwissen“, „Schulangst, Prüfungsangst“, „falsch gelernt“, „mangelnde Begabung“ und „persönliche (z.B. familiäre) Gründe“ geladen. Es handelt sich also um Ursachen, für die der Schüler nicht selbst oder zumindest nicht bewußt verantwortlich ist; ich nenne diesen Faktor daher „Umstände“.
Der dritte Faktor umfaßt hauptsächlich die Gründe „Mathematiklehrer/in“ und „sinnlose Hausübungen“, eine untergeordnete Rolle spielt auch „zu wenig / keine Nachhilfe“. Der Schüler macht also diejenigen, die ihm etwas beibringen hätten sollen, für sein Versagen verantwortlich, der Faktor heißt also „Lehrer“.
Insgesamt war die Faktorenanalyse durchaus erfolgreich; jeder der drei Faktoren wird von charakteristischen Variablen stark geladen, jede Variable ist in einem Faktor erfaßt und es gibt nur eine Variable, die mit mehr als einem Faktor nennenswert korreliert, allerdings zeigt sich auch bei dieser eine eindeutige Präferenz für einen der beiden Faktoren. Daß die Angst ebenfalls in zwei Faktoren vertreten ist, beeinträchtigt das Ergebnis keineswegs, da die Korrelation zum ersten Faktor negativ ist; das Verhältnis ist also indirekt.
Eine Untersuchung der charakteristischen Variablen jedes Faktors ergab, daß weit mehr Schüler die Schuld im ersten Faktor („Selbst“) sehen als in den anderen beiden: Während nämlich 129 Schüler (32%) bei den wichtigsten Variablen dieses Faktors („zu wenig gelernt“ und „zu wenig Hausübungen gemacht“) den Wert 1 oder 2 geben, sind es bei den Hauptvariablen des zweiten Faktors („Umstände“) („fehlendes Grundwissen“, „falsch gelernt“ und „Schulangst, Prüfungsangst“) nur 29 (7%) und bei jenen im Faktor 3 („Lehrer“) („sinnlose Hausübungen“ und „Mathematiklehrer/in“) 36 (9%).
Die Unabhängigkeit der durch eine Faktorenanalyse ermittelten Faktoren zeigt sich jedoch auf eindrucksvolle Weise: Von den 129 „Hauptvertretern“ des ersten Faktors geben 91 (das sind 71% davon) noch in mindestens einer nicht zu diesem Faktor gehörenden Variablen den Wert 1.
Erstaunlicherweise besteht nur zwischen „zu wenig gelernt“ und „zu wenig Hausübungen gemacht“ eine hohe Korrelation (0,47); alle anderen Koeffizienten liegen unter 0,30.
Eine getrennte Betrachtung nach Alter, Geschlecht und Schulart zeigt bei Faktor 1 („Selbst“) deutliche Unterschiede zwischen den Altersgruppen und den Geschlechtern; letztere differieren auch bei Faktor 2 („Umstände“). Im dritten Faktor („Lehrer“) weichen keine dieser Vergleichsgruppen nennenswert voneinander ab. Nach Schulart bestehen bei keiner der zehn Variablen und daher auch bei keinem Faktor merkliche Unterschiede.
Im ersten Faktor stimmen obige Abweichungen im großen und ganzen gut mit den Differenzen in den einzelnen Variablen überein, im Faktor 2 zeigen sich jedoch bei drei Variablen („mangelnde Begabung“, „Schulangst, Prüfungsangst“ und „persönliche (z.B. familiäre) Gründe“) darüber hinaus deutliche Diskrepanzen zwischen den Altersgruppen, die jedoch bei Betrachtung des ganzen Faktors verschwimmen.
Auffallend ist, daß „negative“ Schüler in allen zehn vorgegebenen Variablen niedrigere oder annähernd gleiche Werte geben wie „positive“. Ich führe diesen eindeutigen Trend darauf zurück, daß Schüler mit „positiver“ Note weniger das Gefühl haben, „schlechte Leistungen“ erbracht zu haben, und daher alle Ursachen weniger stark verantwortlich machen.
Von Bedeutung ist dieser Unterschied insofern, als bei der Beurteilung obiger Differenzen speziell darauf geachtet werden muß, ob diese nicht zum Großteil in Wirklichkeit von der Zeugnisnote erklärt werden. Diese Gefahr besteht vor allem zwischen den Altersgruppen, da ab-15jährige Schüler merklich schlechtere Noten haben als unter-15jährige. Zwischen den Geschlechtern weichen die Zeugnisnoten hingegen so gut wie gar nicht voneinander ab, die Durchschnittsnoten unterscheiden sich um weniger als ein Tausendstel; eine Beeinflussung kann hier also ausgeschlossen werden.
Zur Signifikanzprüfung der Diskrepanzen im ersten Faktor habe daher eine univariate mehrfaktorielle Kovarianzanalyse mit dem Alter und dem Geschlecht als Faktoren und der Jahreszeugnisnote als Kovariate durchgeführt. Letztere ist zwar nicht intervallskaliert, eine Kovarianzanalyse stellt jedoch die einzige Möglichkeit zur Untersuchung der genannten Einflüsse unter Ausschaltung der Zeugnisnote dar, sodaß über dieses Problem wohl hinweggesehen werden muß. Alle anderen Voraussetzungen sind gut erfüllt, es sind nämlich sowohl die Werte in allen sechs Gruppen ausreichend normalverteilt, als auch die Varianzen nach den Tests von Cochran und Bartlett & Box homogen.
Die Kovarianzanalyse ist insgesamt höchst signifikant, die Wechselwirkung ist nicht signifikant. Der Einfluß der Kovariaten Jahreszeugnisnote ist hoch signifikant, jener der Haupteffekte sogar höchst signifikant. Im einzelnen stellen sich die Unterschiede folgendermaßen dar: Der durchschnittliche Faktorwert des ersten Faktors („Selbst“) der männlichen Schüler liegt um 0,34 unter jenem der weiblichen; diese Abweichung ist hoch signifikant. Zu beachten ist, daß entsprechend den Antwortmöglichkeiten im Fragebogen niedrigere Faktorwerte eine stärkere Zustimmung anzeigen. Die Spannweite des ersten Faktors ist 4,6, die Mittelwertdifferenzen der Faktorwerte sind also diesbezüglich mit Schulnoten vergleichbar. Ab-15jährige Schüler geben im Durchschnitt um 0,60 niedrigere Werte als unter-15jährige; die Differenz ist höchst signifikant.
Die multiple Klassifikationsanalyse bestätigt dieses Bild: Der Einfluß des Alters auf den ersten Faktor wird deutlich größer als jener des Geschlechts gesehen.
Zur Prüfung der Geschlechtsunterschiede beim zweiten Faktor („Umstände“) ist ein t-Test ausreichend, da sich die Zeugnisnoten der beiden Geschlechter – wie gesagt – praktisch nicht unterscheiden, sodaß eine Kovarianzanalyse nicht notwendig ist. Die Werte sind in beiden Geschlechtern annähernd normalverteilt, die Voraussetzung für einen t-Test ist also erfüllt. Weibliche Schülerinnen geben um durchschnittlich 0,40 niedrigere Werte als männliche, die Spannweite des Faktors ist allerdings mit 5,2 deutlich höher als beim ersten. Der t-Test weist die Unterschiede zwischen den Geschlechtern als höchst signifikant aus.
Zumindest bezüglich der Angst wird der Geschlechtsunterschied durch zahlreiche andere Untersuchungen bestätigt. Wie auch ich vertritt jedoch die Mehrzahl der Autoren die Meinung, daß diese Diskrepanz weniger auf eine tatsächlich geringere Ängstlichkeit männlicher Schüler, sondern eher auf ihre mangelnde Bereitschaft, Angst einzugestehen, zurückzuführen ist (vgl. Sarason, Davidson, Lighthall, Waite & Ruebush, 1960, S. 253; Schell, 1972, S. 53; Gärtner-Harnach, 1976, S. 45; Lißmann, 1976, S. 86; Jacobs & Strittmatter, 1979, S. 167; Felber, 1994, S. 65; Schrattenthaler, 1995, S. 30).
Bei den Variablen „mangelnde Begabung“, „Schulangst, Prüfungsangst“ und „persönliche (z.B. familiäre) Gründe“ bestehen darüber hinaus deutliche Differenzen zwischen den Altersgruppen, die jedoch in verschiedene Richtungen gehen: Bei der mangelnden Begabung und den persönlichen Gründen geben ältere Schüler niedrigere Werte, bei der Angst hingegen jüngere. Zur Signifikanzprüfung bietet sich daher eine multivariate Kovarianzanalyse der ersten beiden Variablen und eine univariate der letztgenannten an; als Kovariate ist wieder die Jahreszeugnisnote aufzunehmen.
Die Variablen „mangelnde Begabung“ und „persönliche (z.B. familiäre) Gründe“ korrelieren zwar nicht signifikant (r = 0,06), weshalb eine multivariate Analyse gegenüber zwei univariaten zwar keinen methodischen Vorteil bringt, die Vorgangsweise ist jedoch einfacher. Die Voraussetzungen sind leider nur mangelhaft erfüllt: Die Anpassung an die Normalverteilung ist in beiden Variablen schlecht und der multivariate Test von Box zeigt höchst signifikante Unterschiede zwischen den Varianzen; diese dürften vor allem durch die Variable „persönliche (z.B. familiäre) Gründe“ verursacht werden, da bei dieser die univariaten Tests von Cochran und Bartlett & Box ebenfalls höchst signifikante Abweichungen der Varianzen feststellen, während sie bei der Variable „mangelnde Begabung“ homogene Varianzen ausweisen. Aufgrund der Verletzungen der Voraussetzungen sind die Ergebnisse der Kovarianzanalyse mit einiger Vorsicht zu betrachten.
Der Einfluß der Kovariaten Jahreszeugnisnote ist nicht signifikant; die multivariaten Tests von Pillai, Wilks und Hotelling zeigen alle hoch signifikante Unterschiede zwischen den Zellen. Einzeln betrachtet sind die Differenzen bezüglich der mangelnden Begabung knapp signifikant, die Mittelwerte liegen um 0,36 auseinander (3,23 bei den Ab-15jährigen und 3,59 bei den Unter-15jährigen). Bei den persönlichen Gründen geben die älteren Schüler mit 3,99 durchschnittlich einen um 0,40 niedrigeren Wert als die jüngeren (4,39); dieser Unterschied ist hoch signifikant.
Schließlich habe ich eine univariate Kovarianzanalyse mit der Angst als abhängiger Variable, dem Alter als Faktor und der Jahreszeugnisnote als Kovariate gerechnet. Die Voraussetzungen sind im großen und ganzen erfüllt; die Anpassung an die Normalverteilung ist zwar etwas mangelhaft, die Varianzen sind jedoch sowohl laut Cochran als auch laut Bartlett & Box homogen.
Die Abweichungen sind insgesamt hoch signifikant, der Einfluß der Kovariaten ist hingegen nicht signifikant. Der Mittelwert der Unter-15jährigen ist um 0,53 niedriger als jener der Ab-15jährigen (2,63 zu 3,15), dieser Unterschied ist hoch signifikant.
Zusammenfassend läßt sich festhalten, daß die Mehrzahl der Schüler die Schuld für das Versagen sich selbst zuschreibt, wenngleich außerdem oft noch andere Gründe angeführt werden. Insbesondere machen sich männliche Schüler stärker selbst verantwortlich als weibliche, diese führen im Gegenzug eher diverse „Umstände“ als Ursachen an. Ab-15jährige Schüler sehen die Gründe für ihr Versagen eher im ersten Faktor (also bei sich selbst) als unter-15jährige, außerdem führen sie ihre mangelnde Begabung und persönliche Gründe vermehrt ins Treffen. Jüngere Schüler hingegen fühlen sich in ihren Leistungen stärker von Angst beeinträchtigt.
Im wesentlichen ähnliche Ergebnisse erzielte Mies-Suermann 1971 bei ihrer Untersuchung an 171 Schülern der 8. bis 10. Schulstufe: Auf die Frage nach den Gründen für schulischen Mißerfolg gaben über 40% sinngemäß „Faulheit“ an (vgl. Mies-Suermann, 1975, S. 56).
Laut Höhn ist das auch für Lehrer die Hauptursache der mangelnden Schülerleistungen: „Das Merkmal, das den Lehrern am häufigsten bei ihren schlechten Schülern auffällt, ist nicht etwa, daß sie nichts leisten können, sondern daß sie nicht wollen. In fast der Hälfte aller Schilderungen werden Verhaltensweisen erwähnt, die, mehr oder weniger mild umschrieben, auf das Urteil ›faul‹ hinauslaufen. Erst an zweiter Stelle kommt das Urteil ›Begabungsmangel‹, das auf 44% der schlechten Schüler angewandt wird.“ (Höhn, 1980, S. 55). Das ist das Ergebnis der mündlichen Charakterisierungen ihrer jeweiligen drei leistungsschwächsten Schüler durch 35 Lehrer (3. bis 13. Schulstufe).
Genau gegenläufig antworteten die 26 Lehrer bei der Untersuchung von Scharf 1988 an einer HAK in Graz: Am öftesten nannten sie „mangelhafte Begabung“ (92%) als Grund für Lernschwierigkeiten der Schüler, gefolgt von „schulische Überlastung“ (77%) und erst an dritter Stelle „Faulheit“ (73%). Die 208 befragten Schüler des 1. bis 4. Jahrgangs (9. bis 12. Schulstufe) teilte Scharf danach in G („ohne Lernschwierigkeiten“, gut) und S („mit Lernschwierigkeiten“, schlecht) ein, ob sie im Jahreszeugnis in mindestens einem Gegenstand ein „Genügend“ oder „Nicht genügend“ erwarteten. Von den 169 als S klassifizierten Schülern wurde am öftesten „Faulheit“ als Ursache angegeben (66%), dann „wenig Interesse für diesen Gegenstand“ (64%). Weiters führten 28% „mangelhafte Begabung“ als Grund an, 22% „Probleme mit dem Lehrer“, 15% „Angst“ und 4% „Probleme mit den Eltern“ (vgl. Scharf, 1988, S. 76). Diese Ergebnisse stimmen ungefähr mit den vorliegenden überein.
Feichtinger befragte 1992 die Eltern von ca. 365 8 oberösterreichischen Hauptschülern und kommt zu dem Ergebnis, daß Eltern hauptsächlich Gründe im Bereich der Schule für ein als Mißerfolg aufgefaßtes Schularbeitsergebnis ihres Kindes verantwortlich machen. Mangelnde Anstrengung oder Ausdauer des Schülers werden hingegen als weniger ausschlaggebend erachtet (vgl. Feichtinger, 1992, S. 119).
Bergner sieht im Anführen des Lehrers als Ursache für die eigene schlechte Leistung eher das Suchen nach Ausreden: „Aber nicht jeder Schüler sieht im Mißerfolg seine eigene Schuld. Sie übertünchen ihr Unzufriedenheitsgefühl und die enttäuschten Erfolgswünsche mittels der Schuldzuweisung an den Lehrer oder den Unterricht. Dem Lehrer werden in diesem Zusammenhang Intoleranz, schlechter Führungsstil im Unterricht, komplizierte bzw. konfuse Erklärungsweise und ungerechte, völlig willkürliche Notengebung vorgeworfen. Der Schüler weiß um die Diskrepanz zwischen seinen Wunschvorstellungen und der tatsächlich realisierten Leistung und wäscht sich sozusagen in Unschuld, um seine Stigmatisierung abzuschwächen.“ (Bergner, 1990, S. 24). Das mag zwar in einigen Fällen zutreffen, im großen und ganzen sehe ich jedoch keinen Grund, an der Ehrlichkeit der Antworten zu zweifeln; zweifellos trägt bei einigen Schülern tatsächlich der Lehrer einen großen Teil der Schuld für die schlechten Leistungen.
Aus psychologischer Sicht sind die Gründe, die ein Schüler für seine bisherigen Leistungen verantwortlich macht, für seine zukünftigen besonders wesentlich. Diese subjektiven Ursachenzuschreibungen heißen Attributionen; sie werden meist in zwei Dimensionen geteilt (vgl. Meyer, 1973, S. 88; Weiner, 1973, S. 82; Jopt, 1978, S. 129; Tiedemann, 1978, S. 114; Rheinberg, 1980, S. 54; Pritz-Garger, 1984, S. 28; Landauer, 1985, S. 65; Herkner, 1986, S. 312; Aberschek, 1990, S. 96; Persy, 1990, S.139; Herkner, 1991, S. 45; Feichtinger, 1992, S. 40; Ingenkamp, 1995, S. 228):
- intern – extern: Diese Dimension zeigt an, ob der Schüler die Ursache bei sich selbst oder bei anderen sieht.
- stabil – variabel: Dadurch wird angegeben, ob der Grund über einen längeren Zeitraum hinweg konstant ist oder sich bis zum nächsten Mal bereits verändern kann.
Von den erhobenen drei Faktoren beinhaltet also der erste mit den Variablen „zu wenig gelernt“, „zu wenig Hausübungen gemacht“ und „zu wenig / keine Nachhilfe“ interne variable Attributionen, Faktor 2 enthält hauptsächlich interne stabile Gründe („fehlendes Grundwissen“, „Schulangst, Prüfungsangst“, „falsch gelernt“, „mangelnde Begabung“ und „persönliche (z.B. familiäre) Gründe“), während der dritte Faktor die externen stabilen Ursachen „Mathematiklehrer/in“ und „sinnlose Hausübungen“ zusammenfaßt.
Die Verarbeitung und Überwindung eines Mißerfolges fällt natürlich
leichter, wenn dieser auf variable Ursachen (wie z. B. Pech) zurückgeführt
wird; in diesem Fall besteht nämlich die Hoffnung, daß es nächstes
Mal wieder besser geht. Wird das Versagen jedoch auf stabile Variable (wie z.
B. mangelnde Begabung) zurückgeführt, sieht der Schüler auch
weiterhin wenig Chance auf Erfolg, da dieser subjektiv entscheidende Grund ja
langfristig bestehen bleibt. Infolgedessen resigniert er und der nächste
Mißerfolg ist bereits vorprogrammiert.
Demzufolge ist eine hohe Zustimmung bei Faktor 1 („Selbst“) für
den betroffenen Schüler wesentlich günstiger als bei den anderen beiden
Faktoren.
„17) Besuchst Du diesen Lernkurs freiwillig?“

| Wert: | 1 | 1,5 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 245 | 5 | 69 | 43 | 17 | 15 | 7 |
| Prozent i | 61,1 | 1,2 | 17,2 | 10,7 | 4,2 | 3,7 | 1,7 |
| Prozent g | 62,2 | 1,3 | 17,5 | 10,9 | 4,3 | 3,8 |
Die große Mehrheit der Schüler gibt an, den Kurs freiwillig zu besuchen; 80% geben den Wert 1 oder 2. Lehrer oder Eltern dürften also im großen und ganzen kaum Druck ausüben.
Nach Geschlecht und Schulart bestehen keine nennenswerten Differenzen, sehr wohl jedoch zwischen Schülern mit „positiver“ und solchen mit „negativer“ Jahreszeugnisnote sowie zwischen den Altersgruppen. Da die Anpassung an die Normalverteilung schlecht ist, habe ich die Signifikanzprüfung durch zwei U-Tests mit Korrektur der Irrtumswahrscheinlichkeit vorgenommen.
Überraschenderweise liegt der Mittelwert der „negativen“ Schüler um 0,51 unter jenem der „positiven“ (1,58 bzw. 2,09), die Abweichung ist laut U-Test hoch signifikant. Sogar höchst signifikant ist der Unterschied zwischen jüngeren und älteren Schülern, die durchschnittliche Differenz ist 0,39 (1,52 bei den Ab-15jährigen bzw. 1,91 bei den Unter-15jährigen).
Daß ältere Schüler den Kurs eher freiwillig besuchen als jüngere, ist nicht weiter verwunderlich, da mit zunehmendem Alter alle Entscheidungen selbständiger getroffen werden. Erstaunlich ist jedoch der Unterschied nach der Zeugnisnote. Der Grund dafür könnte sein, daß „negative“ Schüler selbst der Meinung sind, daß ein Kurs für sie das Beste ist, während „positive“ glauben, keine systematische Lernhilfe zu benötigen.
„18) Wer oder was hat Dich dazu beeinflußt, diesen Lernkurs zu besuchen?“
„Mathematiklehrer/in“

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 16 | 16 | 18 | 18 | 331 | 2 |
| Prozent i | 4 | 4 | 4,5 | 4,5 | 82,5 | 0,5 |
| Prozent g | 4 | 4 | 4,5 | 4,5 | 83 |
„andere(r) Lehrer/in“
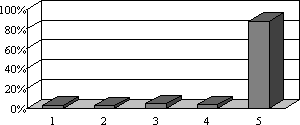

| Wert: | 1 | 2 | 2,5 | 3 | 3,5 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 10 | 8 | 1 | 16 | 1 | 12 | 350 | 3 |
| Prozent i | 2,5 | 2 | 0,2 | 4 | 0,2 | 3 | 87,3 | 0,7 |
| Prozent g | 2,5 | 2 | 0,3 | 4 | 0,3 | 3 | 87,9 |
„Eltern, Erziehungsberechtigte“
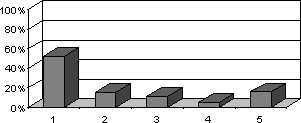

| Wert: | 1 | 2 | 3 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 207 | 62 | 46 | 19 | 1 | 63 | 3 |
| Prozent i | 51,6 | 15,5 | 11,5 | 4,7 | 0,2 | 15,7 | 0,7 |
| Prozent g | 52 | 15,6 | 11,6 | 4,8 | 0,3 | 15,8 |
„Freunde/innen, Kollegen/innen“
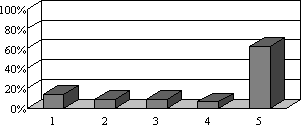

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 54 | 36 | 34 | 25 | 248 | 4 |
| Prozent i | 13,5 | 9 | 8,5 | 6,2 | 61,8 | 1 |
| Prozent g | 13,6 | 9,1 | 8,6 | 6,3 | 62,5 |
„Werbung des Instituts“
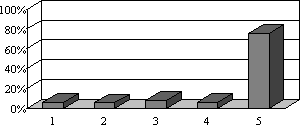

| Wert: | 1 | 2 | 2,5 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 24 | 20 | 1 | 30 | 22 | 300 | 4 |
| Prozent i | 6 | 5 | 0,2 | 7,5 | 5,5 | 74,8 | 1 |
| Prozent g | 6 | 5 | 0,3 | 7,6 | 5,5 | 75,6 |
„etwas anderes / jemand anderer“
| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 17 | 9 | 3 | 0 | 216 | 156 |
| Prozent i | 4,2 | 2,2 | 0,7 | 0 | 53,9 | 38,9 |
| Prozent g | 6,9 | 3,7 | 1,2 | 0 | 88,2 |
„was/wer?“
| Einfluß: | kenne das Institut |
Freundin |
Schwester |
Verwandte |
Direktor |
Bekannte |
Empfehlung |
Jesus |
k.A. |
|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 14 | 3 | 3 | 3 | 2 | 1 | 1 | 1 | 373 |
| Prozent i | 3,5 | 0,7 | 0,7 | 0,7 | 0,5 | 0,2 | 0,2 | 0,2 | 93 |
| Prozent g | 50 | 10,7 | 10,7 | 10,7 | 7,1 | 3,6 | 3,6 | 3,6 |
Der mit Abstand größte Einfluß dürfte von den Eltern ausgehen, die Schüler geben im Durchschnitt den Wert 2,17. Die Mittelwerte aller anderen Variablen liegen über 3,90, ihre Bedeutung scheint also gering.
Erstaunlicherweise ist der Fragenblock weitgehend unabhängig von der vorigen Frage 17 („Besuchst Du diesen Lernkurs freiwillig?“) beantwortet worden; einzig die Maßkorrelation zu „Eltern, Erziehungsberechtigte“ ist mit –0,30 höchst signifikant, alle anderen Koeffizienten liegen unter 0,11.
Ebenso ist die höchst signifikante Korrelation von 0,36 zwischen „Mathematiklehrer/in“ und „andere(r) Lehrer/in“ die einzige über 0,12 innerhalb der fünf vorgegebenen Variablen.
Die getrennte Betrachtung der Vergleichsgruppen zeigte nur bei den Variablen „Eltern, Erziehungsberechtigte“ und „Freunde/innen, Kollegen/innen“ deutliche Unterschiede nach Alter, sowie bei letzterer nach Jahreszeugnisnote. Da beide Variable eindeutig nicht normalverteilt sind, habe ich die Signifikanzprüfung mit drei U-Tests durchgeführt.
Der Einfluß der Eltern wird von den Unter-15jährigen durchschnittlich mit 1,66 bewertet, von den Ab-15jährigen mit 2,53; die Differenz beträgt also 0,87, der Unterschied ist laut U-Test höchst signifikant. Dieses Ergebnis ist gut mit der vorigen Frage 17 („Besuchst Du diesen Lernkurs freiwillig?“) verträglich; dort lag der Mittelwert der jüngeren Schüler ja klar über dem der älteren. Die Beeinflussung durch die Eltern dürfte also insbesondere bei jüngeren Schülern stark sein, diese geben auch an, den Kurs weniger freiwillig zu besuchen.
Etwas weniger stark sind die Abweichungen bei der Variable „Freunde/innen, Kollegen/innen“; hier geben die Ab-15jährigen um durchschnittlich 0,35 niedrigere Werte als die Unter-15jährigen (3,80 bzw. 4,14), Schüler mit „negativer“ Note um 0,46 niedrigere als „Positive“ (3,90 bzw. 4,37). Der Altersunterschied ist gemäß der beiden U-Tests mit Korrektur der Irrtumswahrscheinlichkeit nicht signifikant, die Abweichung nach der Zeugnisnote hingegen schon. Schülern, die im Jahreszeugnis „negativ“ sind, dürfte von Freunden also eher geraten werden, einen Kurs zu besuchen.
„19) Warum besuchst Du diesen Lernkurs?“
„weiß ich selber nicht“

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 15 | 3 | 10 | 12 | 343 | 18 |
| Prozent i | 3,7 | 0,7 | 2,5 | 3 | 85,5 | 4,5 |
| Prozent g | 3,9 | 0,8 | 2,6 | 3,1 | 89,6 |
„wegen der Wiederholungsprüfung“

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 308 | 12 | 8 | 2 | 68 | 3 |
| Prozent i | 76,8 | 3 | 2 | 0,5 | 17 | 0,7 |
| Prozent g | 77,4 | 3 | 2 | 0,5 | 17,1 |
„damit ich in Zukunft besser bin“

| Wert: | 1 | 1,5 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 220 | 1 | 65 | 36 | 16 | 60 | 3 |
| Prozent i | 54,9 | 0,2 | 16,2 | 9 | 4 | 15 | 0,7 |
| Prozent g | 55,3 | 0,3 | 16,3 | 9 | 4 | 15,1 |
„um zu üben“
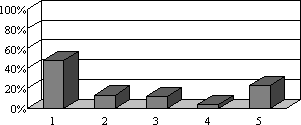

| Wert: | 1 | 2 | 3 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|
| Anzahl | 190 | 52 | 47 | 14 | 1 | 90 | 7 |
| Prozent i | 47,4 | 13 | 11,7 | 3,5 | 0,2 | 22,4 | 1,7 |
| Prozent g | 48,2 | 13,2 | 11,9 | 3,6 | 0,3 | 22,8 |
„weil mir Mathematik Spaß macht“
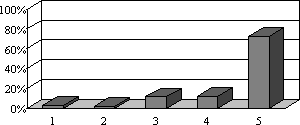

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 9 | 7 | 45 | 48 | 288 | 4 |
| Prozent i | 2,2 | 1,7 | 11,2 | 12 | 71,8 | 1 |
| Prozent g | 2,3 | 1,8 | 11,3 | 12,1 | 72,5 |
„anderer Grund“
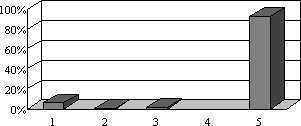
| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 13 | 1 | 3 | 0 | 211 | 173 |
| Prozent i | 3,2 | 0,2 | 0,7 | 0 | 52,6 | 43,1 |
| Prozent g | 5,7 | 0,4 | 1,3 | 0 | 92,5 |
„welcher?“
| Grund: | Matura |
aufholen |
lerne alleine nichts |
Aufnahmeprüfung |
Lernen lernen |
k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 6 | 5 | 5 | 1 | 1 | 383 |
| Prozent i | 1,5 | 1,2 | 1,2 | 0,2 | 0,2 | 95,5 |
| Prozent g | 33,3 | 27,8 | 27,8 | 5,6 | 5,6 |
Erwartungsgemäß ist die bevorstehende Wiederholungsprüfung der Hauptgrund für den Besuch des Kurses, allerdings wollen auch viele in Zukunft besser sein bzw. üben. Die Antwort „weiß ich selber nicht“ wird eindeutig abgelehnt, die große Mehrheit der Schüler sieht also sehr wohl einen Sinn im Kursbesuch. Leider dürfte auch der Spaß an der Mathematik nicht sehr weitverbreitet sein, denn auch bei diesem Grund ist die Zustimmung äußerst gering.
Innerhalb des Fragenblocks besteht nur zwischen „damit ich in Zukunft besser bin“ und „um zu üben“ eine hohe Maßkorrelation (r = 0,60 , höchst signifikant), alle anderen Koeffizienten liegen unter 0,27.
Die Vergleichsgruppen unterscheiden sich teilweise drastisch, so beträgt beispielsweise die Mittelwertdifferenz bei „wegen der Wiederholungsprüfung“ zwischen Schülern mit „positiver“ und solchen mit „negativer“ Zeugnisnote sage und schreibe 3,39 („negative“ Schüler geben im Mittel 1,26, „positive“ 4,65); diese Abweichung ist allerdings nicht sehr überraschend, da ja nur „negative“ Schüler eine Wiederholungsprüfung haben. Bei dieser Variable differieren auch die Altersgruppen deutlich, dabei ist jedoch auf den Einfluß des Jahreszeugnisses zu achten, da ältere Schüler im Mittel schlechtere Noten haben als jüngere. Zur Signifikanzprüfung habe daher ich eine univariate einfaktorielle Kovarianzanalyse vorgenommen.
Weiters bestehen bei den Absichten „damit ich in Zukunft besser bin“ und „um zu üben“ große Unterschiede nach der Zeugnisnote. Da diese beiden Variablen stark korrelieren, ist hier eine multivariate einfaktorielle Varianzanalyse das geeignete Verfahren.
Darüber hinaus unterscheiden sich die Vergleichsgruppen nicht nennenswert voneinander.
Leider sind die Voraussetzungen für die Kovarianzanalyse zur Untersuchung des Altersunterschieds bei der Variablen „wegen der Wiederholungsprüfung“ allesamt nicht erfüllt, die Werte sind in beiden Zellen nicht normalverteilt und die Varianzen nach den Tests von Cochran und Bartlett & Box inhomogen. Die Ergebnisse sind also nur mit Vorsicht zu genießen.
Das Modell insgesamt ist höchst signifikant, ebenso der Einfluß der Kovariaten Jahreszeugnisnote. Die beiden Altersgruppen unterscheiden sich jedoch nicht signifikant.
Auch bei der multivariaten Varianzanalyse von „damit ich in Zukunft besser bin“ und „um zu üben“ mit der Zeugnisnote als Faktor zeigt die Überprüfung der Voraussetzungen ein tristes Bild: Die Normalverteilung ist in beiden Variablen mangelhaft und die Varianzen sind sowohl laut dem multivariaten Test von Box, als auch laut den univariaten von Cochran und Bartlett & Box inhomogen. Die Ergebnisse müssen also wieder mit Vorsicht betrachtet werden.
Die multivariaten Tests von Pillai, Wilks und Hotelling zeigen alle höchst signifikante Differenzen. Im einzelnen bewerten Schüler mit „positiver“ Note den Grund „damit ich in Zukunft besser bin“ um durchschnittlich 0,72 niedriger als ihre „negativen“ Kollegen (die Mittelwerte sind 1,45 und 2,17). Noch stärker ist die Differenz bei „um zu üben“; hier geben „Positive“ sogar um 1,21 niedrigere Werte (1,39 bzw. 2,60). Die Unterschiede sind in beiden Variablen höchst signifikant.
Schüler, die im Zeugnis „negativ“ waren, besuchen den Kurs also hauptsächlich wegen der Wiederholungsprüfung, während „Positive“ vorrangig in das Institut kamen, um in Zukunft bessere Leistungen zu erbringen oder um zu üben.
„20) Was interessiert Dich an Mathematik?“
„nichts, ich will nur durchkommen“
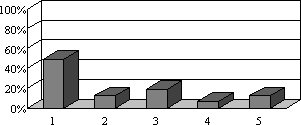
| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 189 | 47 | 71 | 27 | 47 | 20 |
| Prozent i | 47,1 | 11,7 | 17,7 | 6,7 | 11,7 | 5 |
| Prozent g | 49,6 | 12,3 | 18,6 | 7,1 | 12,3 |
„die Regeln zur Beispiellösung“

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 26 | 28 | 82 | 51 | 149 | 65 |
| Prozent i | 6,5 | 7 | 20,4 | 12,7 | 37,2 | 16,2 |
| Prozent g | 7,7 | 8,3 | 24,4 | 15,2 | 44,3 |
„die dahinterliegenden Ideen“

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 43 | 38 | 64 | 45 | 154 | 57 |
| Prozent i | 10,7 | 9,5 | 16 | 11,2 | 38,4 | 14,2 |
| Prozent g | 12,5 | 11 | 18,6 | 13,1 | 44,8 |
Die Interessenslage der Befragten zeigt ein ernüchterndes Bild: Die Mehrheit gibt an, sich für nichts zu interessieren, und zwar weder für die Regeln zur Lösung der Beispiele noch für die dahinterliegenden Ideen.
Alle drei Variablen korrelieren stark und höchst signifikant, die Koeffizienten liegen zwischen 0,45 und 0,52; die Korrelationen von „nichts, ich will nur durchkommen“ mit den anderen beiden Variablen sind natürlich negativ.
Die Betrachtung der Vergleichsgruppen zeigt nur nach der Jahreszeugnisnote deutliche Unterschiede, und zwar bei allen drei Variablen. Zur Signifikanzprüfung bietet sich also eine multivariate einfaktorielle Varianzanalyse an.
Die Voraussetzungen sind leider abermals nur schlecht erfüllt; die Normalverteilung läßt in allen sechs Zellen sehr zu wünschen übrig, und der multivariate Test von Box weist die Unterschiede der Varianzen knapp als signifikant aus, die univariaten Tests von Cochran und Bartlett & Box bestätigen dies bei den Variablen „nichts, ich will nur durchkommen“ und „die dahinterliegenden Ideen“. Lediglich bei „die Regeln zur Beispiellösung“ zeigen sie homogene Varianzen an. Insgesamt sind die Ergebnisse also mit Vorbehalten zu betrachten.
Die Abweichungen zwischen den Zellen sind laut den multivariaten Tests von Pillai, Wilks und Hotelling höchst signifikant. Die größte Mittelwertdifferenz besteht bei „nichts, ich will nur durchkommen“, hier geben „negative“ Schüler um durchschnittlich 0,99 niedrigere Werte als „positive“ (2,06 bzw. 3,05), der Unterschied ist höchst signifikant. Bei den anderen beiden Variablen gehen die Abweichungen in die andere Richtung. So werden „die dahinterliegenden Ideen“ von „Positiven“ im Mittel um 0,53 niedriger bewertet (3,20 bzw. 3,73), die Differenz ist hoch signifikant. Nur knapp signifikant ist hingegen der Unterschied bei „die Regeln zur Beispiellösung“, hier liegen die Mittelwerte um 0,35 auseinander (3,48 bei den „Positiven“ und 3,83 bei den „Negativen“).
„Positive“ Schüler können sich also deutlich mehr für Mathematik begeistern als „negative“; letzteren liegt vermehrt ausschließlich das Durchkommen am Herzen. Insgesamt ist das Interesse für die dahinterliegenden Ideen und sogar für die Regeln zur Lösung der Beispiele im großen und ganzen jedenfalls gering.
„21) Hältst Du den Mathematikunterricht (so wie er bei Dir in der Schule stattfindet) für sinnvoll?“

| Wert: | 1 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 42 | 70 | 1 | 131 | 1 | 55 | 2 | 94 | 5 |
| Prozent i | 10,5 | 17,5 | 0,2 | 32,7 | 0,2 | 13,7 | 0,5 | 23,4 | 1,2 |
| Prozent g | 10,6 | 17,7 | 0,3 | 33,1 | 0,3 | 13,9 | 0,5 | 23,7 |
Wenn schon aus der vorigen Frage 20 („Was interessiert Dich an Mathematik?“) hervorgeht, daß das Interesse an Mathematik durchwegs gering ist, so ist wenigstens der Glaube an die Sinnhaftigkeit des erhaltenen Mathematikunterrichts etwas besser. Zwar geben nur 28% den Wert 1 oder 2, allerdings auch nur 38% 4 oder 5.
Deutliche Unterschiede bestehen nur zwischen jüngeren und älteren Schülern, sowie zwischen jenen mit „positiver“ und „negativer“ Zeugnisnote. Zur näheren Untersuchung habe ich eine univariate zweifaktorielle Varianzanalyse durchgeführt.
Es sind sowohl die Werte in allen vier Gruppen ausreichend normalverteilt, als auch die Varianzen laut den Tests von Cochran und Bartlett & Box homogen, sodaß die Voraussetzungen für die Varianzanalyse erfüllt sind.
Das Ergebnis ist insgesamt höchst signifikant, die Wechselwirkung ist
nicht signifikant. Von den Haupteffekten ist der Einfluß des Alters höchst
signifikant, unter-15jährige Schüler geben im Schnitt um 0,68 niedrigere
Werte als ab-15jährige (die Mittelwerte sind 2,83 und 3,51). Nur knapp
signifikant sind hingegen die Unterschiede nach der Zeugnisnote, die Mittelwertdifferenz
ist 0,49, wobei „positive“ Schüler mit 2,78 niedrigere Werte
geben als „negative“ (3,27).
Auch die multiple Klassifikationsanalyse sieht den Einfluß des Alters
wesentlich stärker als den der Zeugnisnote.
Insgesamt sind also jüngere Schüler stärker von der Sinnhaftigkeit ihres Mathematikunterrichts überzeugt und „positive“ stärker als „negative“.
„22) Hältst Du Mathematik grundsätzlich als Unterrichtsfach für sinnvoll?“
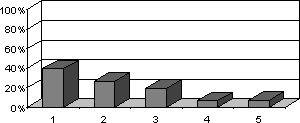

| Wert: | 1 | 1,5 | 2 | 3 | 4 | 4,5 | 5 | k.A. |
|---|---|---|---|---|---|---|---|---|
| Anzahl | 155 | 2 | 104 | 77 | 26 | 1 | 29 | 7 |
| Prozent i | 38,7 | 0,5 | 25,9 | 19,2 | 6,5 | 0,2 | 7,2 | 1,7 |
| Prozent g | 39,3 | 0,5 | 26,4 | 19,5 | 6,6 | 0,3 | 7,4 |
Grundsätzlich wird Mathematik durchaus als sinnvoll angesehen, der Mittelwert ist immerhin 2,16. Im Vergleich zur vorigen Frage (Mittelwert 3,23) zeigt sich eine deutliche Diskrepanz, das Ansehen der Mathematik ist also besser als das des Mathematikunterrichts.
Erstaunlicherweise bestehen nur geringe Unterschiede zwischen den Altersgruppen (Mittelwertdifferenz 0,27), jüngere Schüler sind nur unmerklich stärker von der Sinnhaftigkeit der Mathematik überzeugt. Deutliche Abweichungen zeigen sich hingegen nach Schulart und Jahreszeugnisnote. Da der Vergleich von AHS und BHS nur auf Oberstufenschülern basiert, kann die Signifikanzprüfung der beiden Faktoren nicht gleichzeitig in einer Varianzanalyse erfolgen. Die Normalverteilung ist außerdem schlecht, also habe ich zwei U-Tests mit Korrektur der Irrtumswahrscheinlichkeit vorgenommen.
Der Unterschied zwischen den Schularten ist knapp signifikant, Schüler aus BHS geben um durchschnittlich 0,42 niedrigere Werte als ihre AHS-Kollegen (die Mittelwerte sind 2,02 und 2,43). Die Differenz nach der Zeugnisnote ist etwas stärker; der Mittelwert der „positiven Schüler“ liegt um 0,52 unter dem der „negativen“ (1,68 bzw. 2,20), die Abweichung ist signifikant.
„Positive“ Schüler glauben also sowohl an den Sinn der Mathematik im allgemeinen als auch an den ihres Unterrichts im speziellen stärker als „negative“. Interessant ist, daß die Schüler aus BHS Mathematik für sinnvoller erachten als jene aus AHS; dies könnte daran liegen, daß Mathematik an BHS meist anwendungsorientierter unterrichtet wird und die Nützlichkeit für andere Bereiche viel deutlicher zutage tritt, beispielsweise in den technischen Fächern an der HTL.
„23) Würdest Du es für sinnvoll halten, wenn sich Dein Lehrer mit Dir und Deinen Eltern bereits zu Beginn des zweiten Semesters zusammensetzt, um gemeinsam zu überlegen, wie man ein drohendes „Nicht genügend“ verhindern könnte?“
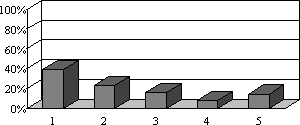

| Wert: | 1 | 2 | 3 | 4 | 5 | k.A. |
|---|---|---|---|---|---|---|
| Anzahl | 156 | 91 | 63 | 31 | 56 | 4 |
| Prozent i | 38,9 | 22,7 | 15,7 | 7,7 | 14 | 1 |
| Prozent g | 39 | 22,9 | 15,9 | 7,8 | 14,1 |
Dieses, in der jüngsten SchUG-Novelle9 enthaltene sogenannte „Frühwarnsystem“, findet bei den Befragten großen Anklang; 61,6% geben den Wert 1 oder 2, nur 21,7% 4 oder 5. Es ersetzt die bisherige Informationspflicht der Erziehungsberechtigten, wenn der Schüler in einem Gegenstand im Jahreszeugnis voraussichtlich mit „Nicht genügend“ zu beurteilen wäre (vulgo „Gefährdung“). Im Vorblatt zur entsprechenden Regierungsvorlage wird die Hoffnung geäußert, daß sich dadurch die Anzahl der Klassenwiederholungen reduziert, unter anderem weil sich die Erziehungsberechtigten durch eine derartige Einladung eher zu einem Gespräch mit dem Lehrer hinreißen lassen, als durch die bisherigen, eher abstoßenden, „blauen Briefe“.
Es besteht nur zwischen den beiden Altersgruppen ein nennenswerter Unterschied; der Mittelwert der Unter-15jährigen liegt bei 2,08, und damit um 0,46 unter dem der Ab-15jährigen (2,54). Die Abweichung ist laut einem U-Test hoch signifikant.
Das Frühwarnsystem wird von den betroffenen Schülern also begrüßt, wobei sich jüngere mit der Idee etwas besser anfreunden können als ältere.
„24) Alter“
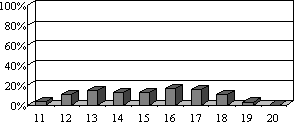

| Alter: | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | k.A. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 14 | 41 | 59 | 50 | 49 | 66 | 63 | 41 | 12 | 2 | 4 |
| Prozent i | 3,5 | 10,2 | 14,7 | 12,5 | 12,2 | 16,5 | 15,7 | 10,2 | 3 | 0,5 | 1 |
| Prozent g | 3,5 | 10,3 | 14,9 | 12,6 | 12,3 | 16,6 | 15,9 | 10,3 | 3 | 0,5 |
„24) Klasse“
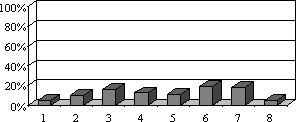

| Klasse: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | k.A. |
|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 21 | 41 | 66 | 52 | 45 | 77 | 71 | 21 | 7 |
| Prozent i | 5,2 | 10,2 | 16,5 | 13 | 11,2 | 19,2 | 17,7 | 5,2 | 1,7 |
| Prozent g | 5,3 | 10,4 | 16,8 | 13,2 | 11,4 | 19,5 | 18 | 5,3 |
Die Klassen wurden ab der 1. Klasse AHS bzw. Hauptschule gezählt, die 2. Klasse entspricht also beispielsweise der 6. Schulstufe.
„24) Geschlecht“

| Geschlecht: | männlich | weiblich | k.A. |
|---|---|---|---|
| Anzahl | 189 | 201 | 11 |
| Prozent i | 47,1 | 50,1 | 2,7 |
| Prozent g | 48,5 | 51,5 |
„25) Schule“
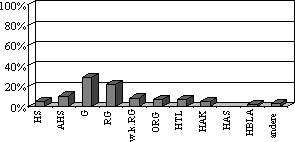

| Schule: | Hauptschule |
AHS (1. oder 2. Klasse) |
Gymnasium |
Realgymnasium |
wirtsch.k. RG |
ORG |
HTL |
HAK |
HAS |
HBLA |
|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 22 | 42 | 115 | 86 | 34 | 27 | 28 | 21 | 0 | 10 |
| Prozent i | 5,5 | 10,5 | 28,7 | 21,4 | 8,5 | 6,7 | 7 | 5,2 | 0 | 2,5 |
| Prozent g | 5,5 | 10,5 | 28,8 | 21,6 | 8,5 | 6,8 | 7 | 5,3 | 0 | 2,5 |
| Schule: | Lehranstalt für Kindergartenpädagogik |
naturwissenschaftliches Realgymnasium |
neusprachliches Gymnasium |
Berufsschule |
Fachschule |
Höhere landwirtschaftliche Bundeslehranstalt |
Institut für Sozialpädagogik |
Versuchsmittelschule |
SMS |
k.A. |
|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 |
| Prozent i | 1,5 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,5 |
| Prozent g | 1,5 | 0,3 | 0,3 | 0,3 | 0,3 | 0,3 | 0,3 | 0,3 | 0,3 |
5 Zusammenfassung
Zahlreiche Untersuchungen beweisen, daß Schulnoten keine der drei klassischen Anforderungen an Messungen, nämlich Objektivität, Reliabilität und Validität, in zufriedenstellendem Maße erfüllen. Die mangelnde Objektivität wurde speziell für Mathematik schon 1913 durch Starch & Elliot nachgewiesen, andere Autoren folgten.
Bei der Leistungsbeurteilung wird in der Pädagogik zwischen drei verschiedenen Bezugsnormen unterschieden: der individuellen, bei der die aktuelle Leistung eines Schülers im Vergleich zu seinen vergangenen bewertet wird, der sozialen, bei der die Leistung in Relation zu der anderer Schüler gesetzt wird, und der sachlichen, bei der die Leistung anhand von vorgegebenen inhaltlichen Kriterien beurteilt wird. Analog dazu kann auch das Versagen auf drei Arten definiert werden: als Nichterbringen einer Mindestanforderung, als deutliches Zurückbleiben hinter dem Durchschnitt und als Nachlassen im Vergleich zu früheren Leistungen.
Ich habe eine empirische Untersuchung mittels Fragebogen (siehe Seite 139) an 401 Schülern durchgeführt, die im Sommer 1996 an einem Wiener Lerninstitut einen Mathematikkurs besucht haben. Die meisten der in Frage kommenden Institute haben sich zur Kooperation bereit erklärt.
Die in einer statistischen Erhebung gesammelten Daten haben je nach Qualität der Meßwerte verschiedene Skalenniveaus. Bei einer Nominalskala unterscheiden sich die einzelnen „Werte“ nur durch verschiedene Namen, bei einer Ordinalskala ist eine Rangreihung möglich, bei einer Intervallskala haben alle aufeinanderfolgenden Werte den selben Abstand und bei einer Rationalskala existiert ein empirischer Nullpunkt.
Die Auswertung der Daten erfolgte mit Hilfe des multiplen Rangkorrelationskoeffizienten von Kendall, der Regressionsanalyse, des t-Tests, des U-Tests, der Varianz- und Kovarianzanalyse, der Faktorenanalyse sowie der Korrektur der Irrtumswahrscheinlichkeit.
Folgende Ergebnisse erscheinen mir besonders bedeutend:
- Der Notendurchschnitt wird von der 1. bis zur 5. Schularbeit immer schlechter, verbessert sich jedoch bei der 6. Schularbeit wieder leicht. Das Jahreszeugnis fällt trotzdem im Schnitt schlechter als alle sechs Schularbeiten aus.
- Im Fall von sechs Schularbeiten läßt sich die Jahreszeugnisnote erstaunlich gut aus den Schularbeitsnoten vorhersagen, knapp drei Viertel der Varianz der Zeugnisnote wird durch die Schularbeiten erklärt. Für das Halbjahreszeugnis ist die Vorhersage zwar weniger treffend, sie erklärt jedoch immer noch mehr als die Hälfte der Varianz.
- Während sich Schüler mit „positiver“ Note im Jahreszeugnis zum Großteil selbst die selbe Note geben würden, die sie tatsächlich erhalten haben, sieht sich die Mehrheit der Schüler mit „negativer“ Note um mindestens eine Notenstufe besser als der Lehrer.
- Ihren Mathematiklehrern geben die Schüler eigentlich ganz gute Noten, der Durchschnitt ist jedenfalls deutlich besser als der der Schülernoten. Entgegen der Meinung einiger Kritiker der Lehrerbeurteilung durch Schüler sind die Noten für den Lehrer de facto unabhängig von der eigenen Note, von der Differenz zwischen tatsächlich erhaltener und selbst gegebener Note sowie vom Anteil der Schüler mit Wiederholungsprüfung in der Klasse, und zwar sowohl bei Unter-15jährigen, als auch bei Ab-15jährigen.
- Die überwiegende Mehrheit der befragten Schüler, die schon einmal eine Klasse wiederholt haben, waren damals auch in Mathematik „negativ“.
- Die errechnete Quote von Schülern mit Wiederholungsprüfung in Mathematik beträgt 19%; dieser Wert liegt aufgrund der Stichprobenbeschaffenheit allerdings mit großer Wahrscheinlichkeit über dem wirklichen.
- Die große Mehrheit der Schüler hat immer oder fast immer eine Mathematikhausübung bekommen.
- Wenn ein Schüler die Hausübung nicht gemacht hat, dann hauptsächlich deshalb, weil sie zu schwer war, oder er keine Lust hatte bzw. zu faul war.
- Mathematik gelernt wurde größtenteils vor Schularbeiten und am Ende des Schuljahres.
- Bei den Ursachen, die die Schüler für ihre schlechten Leistungen verantwortlich machen, lassen sich im wesentlichen drei Gruppen unterscheiden: Gründe, die beim Schüler selbst liegen (z. B. zu wenig gelernt), Gründe, auf die der Schüler keinen direkten Einfluß hat (z. B. mangelnde Begabung) sowie Gründe im Bereich des Lehrers. Zahlenmäßig überwiegt die erste Gruppe, die meisten Schüler sehen die Schuld für ihr Versagen also eher bei sich selbst.
- Fast alle Schüler besuchen den Kurs freiwillig, den größten Einfluß haben die Eltern bzw. Erziehungsberechtigten ausgeübt.
- Schüler mit „negativer“ Jahreszeugnisnote besuchen den Kurs hauptsächlich wegen der Wiederholungsprüfung, solche mit „positiver“ Note, um in Zukunft besser zu sein bzw. um zu üben.
- Das Interesse an der Mathematik ist zwischen diesen Gruppen ebenfalls unterschiedlich: „Negative“ Schüler interessieren sich deutlich mehr als „positive“ gar nicht für Mathematik und wollen eigentlich nur durchkommen.
- Grundsätzlich wird Mathematikunterricht dennoch von den meisten als sinnvoll empfunden, beim tatsächlich erhaltenen Mathematikunterricht ist diese Zustimmung allerdings deutlich geringer.
- Das kürzlich in Kraft getretene „Frühwarnsystem“ zur Verringerung der Klassenwiederholungen findet bei den Befragten größtenteils Anklang.
Anhang 1: Fragebogen
Thomas Landauer
Fragebogen
Im Rahmen meiner Diplomarbeit an der Universität Wien untersuche ich Schüler/innen, die Schwierigkeiten in Mathematik haben. Dazu bitte ich Dich um Deine Mithilfe:
Bitte füll diesen Fragebogen ehrlich aus. Deine Antworten werden anonym ausgewertet und an niemanden weitergegeben. Die Untersuchung dient reinen Forschungszwecken.
Solltest Du bei einigen Fragen keine genauen Angaben machen können, so versuche bitte zu schätzen.
- Was waren Deine Noten in Mathematik im abgelaufenen Schuljahr?
Gegebenenfalls einige Schularbeiten streichen, Semesteraufteilung aber bitte beachten!
- n: nicht beurteilt
- v: versäumt
- 1. Schularbeit

- 2. Schularbeit

- 3. Schularbeit

- Halbjahreszeugnis

- 4. Schularbeit

- 5. Schularbeit

- 6. Schularbeit

- Jahreszeugnis

- Welche Note würdest Du Dir selbst im Jahreszeugnis geben?

- Welche Note würdest Du Deinem/r Mathematiklehrer/in geben?

- Wie oft hast Du schon eine Klasse wiederholt?
 mal
mal - Wie oft davon warst Du auch in Mathematik negativ?
 mal
mal - In wie vielen Fächern hast Du eine Wiederholungsprüfung („Nachzipf“)?

- Darfst Du in jedem Fall aufsteigen (mit „Klausel“)? ❍ Ja ❍ Nein
- Wie viele Schüler/innen in Deiner Klasse haben eine
Wiederholungsprüfung in Mathematik (Dich eingerechnet)? - Wie viele Schüler/innen gehen in Deine Klasse (Dich eingerechnet)?
Kreuze nun bitte in jeder Zeile etwas an! Erläuterungen findest Du im Kästchen rechts.
- Immer: 1
- Nie: 5
- Wie hast Du im Mathematikunterricht aufgepaßt?

- Wie oft habt Ihr in Mathematik eine Hausübung bekommen?

- Wie oft hast Du die Hausübung (selbst!) gemacht?

- Wenn Du die Hausübung nicht (selbst) gemacht hast, warum nicht?
- Trifft voll zu: 1
- Trifft gar nicht zu: 5
- Sie war mir zu schwer

- Sie erschien mir sinnlos

- Sie wurde nicht kontrolliert

- Sie hatte keinen Einfluß auf die Note

- Ich habe keine Zeit gehabt

- anderer Grund
 welcher?
welcher?
- Was hältst Du davon, wenn nicht alle Schüler/innen die selbe Hausübung
bekommen, sondern eine an ihr Können angepaßte?- Sehr viel: 1
- Gar nichts: 5

- Wann hast Du im abgelaufenen Schuljahr Mathematik gelernt?
- Sehr viel gelernt: 1
- Gar nicht gelernt: 5
- regelmäßig

- vor Schularbeiten

- am Ende des ersten Semesters

- am Ende des zweiten Semesters

- wann anders
 wann?
wann?
- Welche Ursachen machst Du für Deine schlechten Leistungen in Mathematik verantwortlich?
- Sehr: 1
- Gar nicht: 5
- fehlendes Grundwissen

- falsch gelernt

- zu wenig gelernt

- zu wenig / keine Nachhilfe

- sinnlose Hausübungen

- zu wenig Hausübungen gemacht

- mangelnde Begabung

- Mathematiklehrer/in

- Schulangst, Prüfungsangst

- persönliche (z.B. familiäre) Gründe

- etwas anderes
 was?
was?
- Besuchst Du diesen Lernkurs freiwillig?
- Ganz freiwillig: 1
- Ganz unfreiwillig: 5

- Wer oder was hat Dich dazu beeinflußt, diesen Lernkurs zu besuchen?
- Sehr beeinflußt: 1
- Gar nicht beeinflußt: 5
- Mathematiklehrer/in

- andere(r) Lehrer/in

- Eltern, Erziehungsberechtigte

- Freunde/innen, Kollegen/innen

- Werbung des Instituts

- etwas anderes / jemand anderer
 was/wer?
was/wer?
- Warum besuchst Du diesen Lernkurs?
- Sehr: 1
- Gar nicht: 5
- weiß ich selber nicht

- wegen der Wiederholungsprüfung

- damit ich in Zukunft besser bin

- um zu üben

- weil mir Mathematik Spaß macht

- anderer Grund
 welcher?
welcher?
- Was interessiert Dich an Mathematik?
- Sehr: 1
- Gar nicht: 5
- nichts, ich will nur durchkommen

- die Regeln zur Beispiellösung

- die dahinterliegenden Ideen

- Hältst Du den Mathematikunterricht (so wie er bei Dir
in der Schule stattfindet) für sinnvoll?- Sehr sinnvoll: 1
- Gar nicht sinnvoll: 5

- Hältst Du Mathematik grundsätzlich als Unterrichtsfach
für sinnvoll (bei gutem Unterricht)?- Sehr sinnvoll: 1
- Gar nicht sinnvoll: 5

- Würdest Du es für sinnvoll halten, wenn sich Dein Lehrer mit Dir und Deinen Eltern bereits zu
Beginn des zweiten Semesters zusammensetzt, um gemein-
sam zu überlegen, wie man ein drohendes „Nicht genügend“
verhindern könnte?- Ja, sehr: 1
- Nein, gar nicht: 5

- Alter: Klasse: Geschlecht: ❍ männlich ❍ weiblich
-
Schule: ❍ Hauptschule ❍ AHS (1. oder 2. Klasse) ❍ Gymnasium ❍ Realgymnasium ❍ wirtsch.k. RG ❍ ORG ❍ HTL ❍ HAK ❍ HAS ❍ HBLA ❍ andere: (bitte ausschreiben)
Anhang 2: Programme
Die folgenden beiden Programme zur Berechnung von multiplen Rangkorrelationskoeffizienten habe ich in Derive 3.00 programmiert.
T(a,b), T2(a,b), … T6(a,b) stehen für τab
und dienen zur Eingabe der von SPSS berechneten bivariaten Rangkorrelationskoeffizienten.
Die Unterteilung in T, T2, … T6 war notwendig, um die maximale Zeilenlänge
von Derive nicht zu überschreiten. Die umgekehrte Reihenfolge ist beabsichtigt,
da sonst z. B. bei der Definition von T2 auf das noch unbekannte T3 verwiesen
wird.
„TP“ steht für „τ
partiell“; die Zahl gibt die Anzahl der korrelierten Variablen an. TP6(a,b,c,d,e,f)
steht also beispielsweise für τab·cdefg
. Auch hier ist die Reihenfolge der Eingabe zu beachten.
„TM“ schließlich steht für „τ
multipel“; die Zahl gibt wieder die Anzahl der korrelierten Variablen
an. TM7(a,b,c,d,e,f,g) steht also für τa·bcdefg
.
Die Tilden („~“) sind nur notwendig, wenn die Programme im reinen Text-Format als MTH-Dateien gespeichert und in Derive geladen werden.
Reihenfolge der Variablen in Programm 1 (Halbjahreszeugnis):
1 Halbjahreszeugnis
2 1. Schularbeit
3 2. Schularbeit
4 3. Schularbeit
Reihenfolge der Variablen in Programm 2 (Jahreszeugnis):
1 Jahreszeugnis
2 1. Schularbeit
3 2. Schularbeit
4 3. Schularbeit
5 4. Schularbeit
6 5. Schularbeit
7 6. Schularbeit
Programm 1 (Halbjahreszeugnis)
T(a,b):=IF(a>b,T(b,a),IF(a=1,IF(b=2,0.3142,IF(b=3,0.2809,IF(b=4,0.5849,x),x),x~
),IF(a=2,IF(b=3,0.2537,IF(b=4,0.5235,x),x),IF(a=3,IF(b=4,0.4903,x),x),x),x),x)
TP3(a,b,c):=(T(a,b)-T(a,c)*T(b,c))/((1-T(a,c)^2)*(1-T(b,c)^2))^(1/2)
TP4(a,b,c,d):=(TP3(a,b,d)-TP3(a,c,d)*TP3(b,c,d))/((1-TP3(a,c,d)^2)*(1-TP3(b,c,~
d)^2))^(1/2)
TM4(a,b,c,d):=(1-(1-T(a,b)^2)*(1-TP3(a,c,b)^2)*(1-TP4(a,d,b,c)^2))^(1/2)
Programm 2 (Jahreszeugnis)
T6(a,b):=IF(a>b,T6(b,a),IF(a=6,IF(b=7,0.2986,x),x))
T5(a,b):=IF(a>b,T5(b,a),IF(a=5,IF(b=6,0.143,IF(b=7,0.1609,x),x),T6(a,b)))
T4(a,b):=IF(a>b,T4(b,a),IF(a=4,IF(b=5,0.1834,IF(b=6,0.2214,IF(b=7,0.3012,x),x)~
,x),T5(a,b)))
T3(a,b):=IF(a>b,T3(b,a),IF(a=3,IF(b=4,0.2537,IF(b=5,0.2054,IF(b=6,0.1035,IF(b=~
7,0.1835,x),x),x),x),T4(a,b)))
T2(a,b):=IF(a>b,T2(b,a),IF(a=2,IF(b=3,0.3142,IF(b=4,0.2809,IF(b=5,0.1802,IF(b=~
6,0.1622,IF(b=7,0.1868,x),x),x),x),x),T3(a,b)))
T(a,b):=IF(a>b,T(b,a),IF(a=1,IF(b=2,0.276,IF(b=3,0.2547,IF(b=4,0.2834,IF(b=5,0~
.3749,IF(b=6,0.4209,IF(b=7,0.54,x),x),x),x),x),x),T2(a,b)))
TP3(a,b,c):=(T(a,b)-T(a,c)*T(b,c))/((1-T(a,c)^2)*(1-T(b,c)^2))^(1/2)
TP4(a,b,c,d):=(TP3(a,b,d)-TP3(a,c,d)*TP3(b,c,d))/((1-TP3(a,c,d)^2)*(1-TP3(b,c,~
d)^2))^(1/2)
TP5(a,b,c,d,e):=(TP4(a,b,d,e)-TP4(a,c,d,e)*TP4(b,c,d,e))/((1-TP4(a,c,d,e)^2)*(~
1-TP4(b,c,d,e)^2))^(1/2)
TP6(a,b,c,d,e,f):=(TP5(a,b,d,e,f)-TP5(a,c,d,e,f)*TP5(b,c,d,e,f))/((1-TP5(a,c,d~
,e,f)^2)*(1-TP5(b,c,d,e,f)^2))^(1/2)
TP7(a,b,c,d,e,f,g):=(TP6(a,b,d,e,f,g)-TP6(a,c,d,e,f,g)*TP6(b,c,d,e,f,g))/((1-T~
P6(a,c,d,e,f,g)^2)*(1-TP6(b,c,d,e,f,g)^2))^(1/2)
TM7(a,b,c,d,e,f,g):=(1-(1-T(a,b)^2)*(1-TP3(a,c,b)^2)*(1-TP4(a,d,b,c)^2)*(1-TP5~
(a,e,b,c,d)^2)*(1-TP6(a,f,b,c,d,e)^2)*(1-TP7(a,g,b,c,d,e,f)^2))^(1/2)
Abkürzungsverzeichnis
| AHS | allgemeinbildende höhere Schule |
| BGBl. | Bundesgesetzblatt |
| BMHS | berufsbildende mittlere bzw. höhere Schule |
| bzw. | beziehungsweise |
| d. h. | das heißt |
| gestr. | gestrichen |
| HAK | Handelsakademie |
| HAS | Handelsschule |
| HBLA | Höhere Bundeslehranstalt für wirtschaftliche Berufe |
| Hjz | Halbjahreszeugnis (Schulnachricht) |
| HTL | Höhere technische Lehranstalt |
| HÜ | Hausübung |
| Jz | Jahreszeugnis |
| k.A. | keine Angabe |
| n.b. | nicht beurteilt |
| ORG | Oberstufenrealgymnasium |
| Prozent g | Prozent gültig (Prozent bezogen auf gültige Antworten) |
| Prozent i | Prozent insgesamt (Prozent bezogen auf alle Antworten) |
| S. | Seite |
| SA | Schularbeit |
| SchUG | Schulunterrichtsgesetz |
| vers. | versäumt |
| wirtsch.k. RG | wirtschaftskundliches Realgymnasium |
| z. B. | zum Beispiel |
Literaturverzeichnis
- Aberschek Kurt: Bewältigungsstrategien bei schulischem Mißerfolg – in Abhängigkeit von Kausalattribution, Geschlecht und Schulleistung. Diplomarbeit an der Naturwissenschaftlichen Fakultät der Universität Salzburg, 1990
- Backhaus Klaus, Erichson Bernd, Plinke Wulff & Weiber Rolf: Multivariate Analysemethoden — Eine anwendungsorientierte Einführung. 8. Auflage, Berlin / Heidelberg / New York: Springer-Verlag, 1996
- Bergner Ingrid: Leistungsversagen in der Schule. Diplomarbeit am Institut für Schulpädagogik und Sozialpädagogik der Universität für Bildungswissenschaften Klagenfurt, 1990
- Birkel Peter: Schriftliche Prüfungen durch Klassenarbeiten. In: Heller Kurt (Hrsg.): Leistungsdiagnostik in der Schule. 4. Auflage, Bern: Verlag Hans Huber, 1984, S. 237 – 244
- Brachinger Hans & Ost Friedmann: Modelle mit latenten Variablen: Faktorenanalyse, Latent-Structure-Analyse und LISREL-Analyse. In: Fahrmeir Ludwig, Hamerle Alfred & Tutz Gerhard (Hrsg.): Multivariate statistische Verfahren. 2. Auflage, Berlin: Verlag Walter de Gruyter, 1996, S. 639 – 766
- Brosius Gerhard & Brosius Felix: SPSS — Base System und Professional Statistics. 1. Auflage, Bonn: International Thomson Publishing, 1995
- Buchacher Robert: Der Club der Noten-Dichter. In: Profil — Das unabhängige Nachrichtenmagazin Österreichs, Nr. 36, 1995 (26. Jahrgang), S. 64 – 70
- Bühl Achim & Zöfel Peter: SPSS für Windows Version 6.1 — Praxisorientierte Einführung in die moderne Datenanalyse. 2. Auflage, Bonn: Verlag Addison-Wesley, 1995
- Clauß Günter & Ebner Heinz: Grundlagen. 7. Auflage, Thun / Frankfurt: Verlag Harri Deutsch, 1992 (Reihe: Statistik - Für Soziologen, Pädagogen, Psychologen und Mediziner, Band 1)
- Clauß Günter, Finze Falk-Rüdiger & Partzsch Lothar: Grundlagen. Thun / Frankfurt: Verlag Harri Deutsch, 1994 (Reihe: Statistik — Für Soziologen, Pädagogen, Psychologen und Mediziner, Band 1)
- Dicker Heinz: Die Reliabilität der Beurteilung von Mathematikarbeiten. In: Ingenkamp Karlheinz (Hrsg.): Die Fragwürdigkeit der Zensurengebung — Texte und Untersuchungsberichte. 8. Auflage, Weinheim / Basel: Beltz Verlag, 1989, S. 173 – 176 (leicht gekürzt auch in: Ingenkamp Karlheinz (Hrsg.): Schüler- und Lehrerbeurteilung — Empirische Untersuchungen zur pädagogischen Diagnostik. Weinheim / Basel: Beltz Verlag, 1977, S. 186 – 188)
- Diehl Jörg & Kohr Heinz: Deskriptive Statistik. 9. Auflage, Eschborn bei Frankfurt: Verlag Dietmar Klotz, 1991
- Dumke Dietrich: Schülerleistung und Zensur. Hannover: Hermann Schroedel Verlag, 1973 (Reihe: Ergebnisse aus der Arbeit der Niedersächsischen Lehrerfortbildung, Heft 23)
- Engelmayer Otto: Schulversagen. In: Horney Walter, Ruppert Johann & Schultze Walter (Hrsg.): Pädagogisches Lexikon — in zwei Bänden. Gütersloh: Bertelsmann Fachverlag, 1970, S. 959
- Fahrmeir Ludwig & Hamerle Alfred: Einführung. In: Fahrmeir Ludwig, Hamerle Alfred & Tutz Gerhard (Hrsg.): Multivariate statistische Verfahren. 2. Auflage, Berlin / New York: Verlag de Gruyter, 1996, S. 1 – 17
- Fahrmeir Ludwig, Hamerle Alfred & Nagl Willi: Varianz- und Kovarianzanalyse. In: Fahrmeir Ludwig, Hamerle Alfred & Tutz Gerhard (Hrsg.): Multivariate statistische Verfahren. 2. Auflage, Berlin: Verlag Walter de Gruyter, 1996, S. 169 – 238
- Fahrmeir Ludwig, Kaufmann Heinz & Kredler Christian: Regressionsanalyse. In: Fahrmeir Ludwig, Hamerle Alfred & Tutz Gerhard (Hrsg.): Multivariate statistische Verfahren. 2. Auflage, Berlin: Verlag Walter de Gruyter, 1996, S. 93 – 168
- Feichtinger Renate: Elternreaktion auf Schulleistung — Eine empirische Studie über elterliche Ursachenzuschreibungen von Schulleistung und ihre Reaktion darauf. Hauptband und Anhang, Diplomarbeit an der Geisteswissenschaftlichen Fakultät der Universität Salzburg, 1992
- Felber Karin: Schulangst in Mathematik — Ihre Entstehung sowie Maßnahmen zur Angstreduktion durch schülerorientierten Mathematikunterricht. Diplomarbeit an der Grund- und Integrativwissenschaftlichen Fakultät der Universität Wien, 1994
- Fischer Gerhard: Statistische Auswertung psychologischer Experimente I — Skriptum zur Vorlesung im WS. 4. Auflage, Institut für Psychologie der Universität Wien: Selbstverlag des Autors, 1991
- Fischer Gerhard: Statistische Auswertung psychologischer Experimente II — Skriptum zur gleichnamigen Vorlesung im Sommersemester. 2. Auflage, Institut für Psychologie der Universität Wien: Selbstverlag des Autors, 1992
- Garnitschnig Karl: Verbale Beurteilung und Unterrichtsgestaltung. In: Olechowski Richard & Rieder Karin (Hrsg.): Motivieren ohne Noten. Wien / München: Jugend und Volk Verlag, 1990 (Reihe: Schule – Wissenschaft – Politik, Band 3), S. 174 – 205
- Gärtner-Harnach Viola: Angst und Leistung. 3. Auflage, Weinheim / Basel: Beltz Verlag, 1976
- Grotefent Robert: Das Problem des Leistungsschwachen im Sportunterricht — Freistellung oder pädagogische Hilfe? In: Leibeserziehung 19, 1969, 3, S. 80 – 86. Zitiert nach Melber, 1988, S. 15
- Güttler Peter: Statistik mit SPSS/PC+ und SPSS für Windows — Einführung für Sozialpädagogen, Psychologen und Erziehungswissenschaftler. 2. Auflage, München: Oldenbourg Verlag, 1996
- Hanisch Günter: Problematik der Leistungsfeststellung durch schriftliche Arbeiten am Beispiel der Mathematik. Habilitationsschrift an der Grund- und Integrativwissenschaftlichen Fakultät der Universität Wien, 1990 (Reihe: Schule – Wissenschaft – Politik, Band 5)
- Hartung Joachim & Elpelt Bärbel: Multivariate Statistik — Lehr- und Handbuch der angewandten Statistik. 4. Auflage, München: Oldenbourg Verlag, 1992
- Hartung Joachim, Elpelt Bärbel & Klösener Karl-Heinz: Statistik — Lehr- und Handbuch der angewandten Statistik. 9. Auflage, München: Oldenbourg Verlag, 1993
- Heckhausen Heinz: Motivation und Handeln — Lehrbuch der Motivationspsychologie. Berlin / Heidelberg / New York: Springer Verlag, 1980
- Heiler Siegfried & Michels Paul: Deskriptive und Explorative Datenanalyse. München: Oldenbourg Verlag, 1994
- Herkner Werner: Psychologie. Wien: Springer-Verlag, 1986
- Herkner Werner: Lehrbuch Sozialpsychologie. 1. Auflage, Bern: Verlag Hans Huber, 1991
- Höhn Elfriede: Der schlechte Schüler — Sozialpsychologische Untersuchungen über das Bild des Schulversagers. Neuausgabe, München: R. Piper & Co Verlag, 1980
- Hoschek Adolf: Der leistungsschwache Schüler in den Leibesübungen — Sportpädagogische und medizinische Analysen aus der Sicht des Leibeserziehers und des Schularztes. In: Leibesübungen-Leibeserziehung, Heft 10, 1983 (37. Jahrgang), S. 227 – 231
- Ingenkamp Karlheinz: Zur Problematik der Zensurengebung. In: Schwarzer Christine & Schwarzer Ralf (Hrsg.): Diagnostik im Schulwesen — Studientexte zur pädagogischen Diagnose, Beratung und Entscheidung. 1. Auflage, Braunschweig: Westermann Verlag, 1977 (Reihe: Psychologie und Erziehung), S. 15 – 36
- Ingenkamp Karlheinz: Lehrbuch der pädagogischen Diagnostik — Studienausgabe. 3. Auflage, Weinheim / Basel: Beltz Verlag, 1995
- Ingenkamp Karlheinz (Hrsg.): Die Fragwürdigkeit der Zensurengebung — Texte und Untersuchungsberichte. 8. Auflage, Weinheim / Basel: Beltz Verlag, 1989
- Jacobs Bernhard & Strittmatter Peter: Der schulängstliche Schüler — Eine empirische Untersuchung über mögliche Ursachen und Konsequenzen der Schulangst. München / Wien / Baltimore: Verlag Urban & Schwarzenberg, 1979
- Janssen Jürgen & Laatz Wilfried: Statistische Datenanalyse mit SPSS für Windows — Eine anwendungsorientierte Einführung in das Basissystem. Heidelberg: Springer-Verlag, 1994
- Jopt Uwe-Jörg: Selbstkonzept und Ursachenerklärung in der Schule — Zur Attribuierung von Schulleistungen. Bochum: Verlag Ferdinand Kamp, 1978
- Jugend-Info der Stadt Wien – Wiener Jugendkreis / MA 13 – Landesjugendreferat Wien (Hrsg.): Nachhilfe — Info-Blatt Nr. 4/96, 2. Auflage, 1996
- Klauer Karl: Fördernde Notengebung durch Benotung unter drei Bezugsnormen. In: Olechowski Richard & Persy Elisabeth (Hrsg.): Fördernde Leistungsbeurteilung — Ein Symposion. Wien / München: Jugend und Volk Verlag, 1987 (Reihe: Schule – Wissenschaft – Politik, Band 1), S. 180 – 206
- Kozmut Irmgard: Schulversagen – eine Problemstellung mit zweifachem Hintergrund. Diplomarbeit am Institut für Erziehungswissenschaften der Universität Graz, 1988
- Krapp Andreas: Forschungsergebnisse zur Bedingungsstruktur der Schulleistung. In: Heller Kurt (Hrsg.): Leistungsdiagnostik in der Schule. 4. Auflage, Bern: Verlag Hans Huber, 1984, S. 46 – 62
- Landauer Doris: Psychische Folgen der Arbeitslosigkeit. Diplomarbeit an der Grund- und Integrativwissenschaftlichen Fakultät der Universität Wien, 1985
- Langfeldt Hans-Peter: Die klassische Testtheorie als Grundlage normorientierter (standardisierter) Schulleistungstests. In: Heller Kurt (Hrsg.): Leistungsdiagnostik in der Schule. 4. Auflage, Bern: Verlag Hans Huber, 1984, S. 65 – 98
- Lißmann Urban: Schulleistung und Schulangst — Eine multivariate Untersuchung im 5. Schuljahr in Gesamtschulen. Weinheim / Basel: Beltz Verlag, 1976
- Matschinger Claudia: Hausübungen im Mathematikunterricht — Eine empirische Untersuchung. Diplomarbeit an der Formal- und Naturwissenschaftlichen Fakultät der Universität Wien, 1994
- Melber Claudia: Zum Problem leistungsschwacher Schüler in den Leibesübungen — Eine empirische Untersuchung der unverbindlichen Übung zur Förderung leistungsschwacher Schüler an Wiener AHS. Diplomarbeit an der Grund- und Integrativwissenschaftlichen Fakultät der Universität Wien, 1988
- Meyer Wulf-Uwe: Leistungsmotiv und Ursachenerklärung von Erfolg und Mißerfolg. 1. Auflage, Stuttgart: Ernst Klett Verlag, 1973
- Mies-Suermann Irmela: Untersuchungen zum Leistungsversagen bei Gymnasiasten. Dissertation an der Philosophischen Fakultät der Universität Bonn, 1975
- Norušis Marija: SPSS/PC+ Advanced Statistics 4.0 — for the IBM PC/XT/AT and PS/2. Chicago: SPSS Inc., 1990
- Norušis Marija: SPSS — SPSS for Windows Professional Statistics Release 5. Chicago: SPSS Inc., 1992
- Ossimitz Günther: Leistungsbeurteilung als Reduktion. In: Dörfler Willibald & Fischer Roland (Hrsg.): Empirische Untersuchungen zum Lehren und Lernen von Mathematik. (Schriftenreihe Didaktik der Mathematik, Universität für Bildungswissenschaften in Klagenfurt, Band 10) Wien: Verlag Hölder-Pichler-Tempsky, 1985, S. 199 – 206
- Persy Elisabeth: Auswirkungen der Leistungsbeurteilung auf Merkmale der Schülerpersönlichkeit. In: Olechowski Richard & Rieder Karin (Hrsg.): Motivieren ohne Noten. Wien / München: Jugend und Volk Verlag, 1990 (Reihe: Schule – Wissenschaft – Politik, Band 3), S. 129 – 171
- Pritz-Garger Brigitte: Psychosoziale Dimensionen des Schulversagens — Eine attributionstheoretische Untersuchung an einer Allgemeinbildenden Höheren Schule in Wien. Dissertation an der Grund- und Integrativwissenschaftlichen Fakultät der Universität Wien, 1984
- Reichel Hans-Christian, Hanisch Günter & Müller Robert: Wahrscheinlichkeitsrechnung und Statistik. 3. Auflage, Wien: Verlag Hölder-Pichler-Tempsky, 1992 (Reihe: Mathematik für Schule und Praxis, Band 1)
- Rheinberg Falko: Leistungsbewertung und Lernmotivation. Göttingen: Verlag für Psychologie Hogrefe, 1980 (Reihe: Motivationsforschung, Band 8)
- Rheinberg Falko: Soziale versus individuelle Leistungsvergleiche und ihre motivationalen Folgen in Lehr-Lernsituationen. In: Olechowski Richard & Persy Elisabeth (Hrsg.): Fördernde Leistungsbeurteilung — Ein Symposion. Wien / München: Jugend und Volk Verlag, 1987 (Reihe: Schule – Wissenschaft – Politik, Band 1), S. 80 – 115
- Rieder Karin: Problematik der Notengebung. In: Olechowski Richard & Rieder Karin (Hrsg.): Motivieren ohne Noten. Wien / München: Jugend und Volk Verlag, 1990 (Reihe: Schule – Wissenschaft – Politik, Band 3), S. 16 – 55
- Röhr Michael, Lohse Heinz & Ludwig Rolf: Statistische Verfahren. Thun / Frankfurt: Verlag Harri Deutsch, 1983 (Reihe: Statistik — Für Soziologen, Pädagogen, Psychologen und Mediziner, Band 2)
- Sacher Werner: Praxis der Notengebung — Hilfen für den Schulalltag. Bad Heilbrunn: Verlag Julius Klinkhardt, 1984
- Sacher Werner: Schulleistung — Forderung, Überprüfung, Beurteilung. Akademiebericht Nr. 178 der Akademie für Lehrerfortbildung Dillingen, 1991
- Sarason Seymour, Davidson Kenneth, Lighthall Frederick, Waite Richard & Ruebush Britton: Anxiety in elementary school children — A report of research. New York / London: John Wiley & Sons Verlag, 1960
- Scharf Christine: Schulversagen an berufsbildenden mittleren und höheren Schulen (Ursachen und Folgen) — Empirische Untersuchung mittels Fragebögen. Diplomarbeit am Institut für Erziehungswissenschaften der Universität Graz, 1988
- Schell Hans: Angst und Schulleistung. Göttingen: Verlag für Psychologie, Hogrefe, 1972
- Schrattenthaler Christina: Schulangst, Lern- und Merkfähigkeit und Konzentration — Eine empirische Untersuchung in einer Hauptschule. Diplomarbeit an der Naturwissenschaftlichen Fakultät der Universität Innsbruck, 1995
- Schwarzer Christine: Gestörte Lernprozesse — Analyse von Leistungsschwierigkeiten im Schulsystem. München / Wien / Baltimore: Urban & Schwarzenberg Verlag, 1980
- Schwendenwein Werner: Erfolg und Versagen in technischen Schulen — Eine empirische Untersuchung potentieller Ingenieure und Techniker. 1. Auflage, Wien: Österreichischer Bundesverlag, 1982 (Reihe: Schriften zur Lehrerbildung und Lehrerfortbildung, Band 28)
- Seidl Peter: Versager auf höheren Schulen — Eine empirische Untersuchung an vier Innsbrucker Gymnasien. Dissertation an der Philosophischen Fakultät der Universität Salzburg, 1967
- Seyfried Helmut: Ergebnisse von Schülerbefragungen. Bregenz: Vervielfältigt, 1980. Zitiert nach Weiss, 1989 a, S. 106
- Starch D. & Elliot E.: Die Verläßlichkeit der Zensuren von Mathematikarbeiten. Übersetzt von Karin Tzschätzsch. In: Ingenkamp Karlheinz (Hrsg.): Die Fragwürdigkeit der Zensurengebung — Texte und Untersuchungsberichte. 8. Auflage, Weinheim / Basel: Beltz Verlag, 1989, S. 81 – 89 (vollständige Wiedergabe des Artikels: Reliability of grading work in mathematics. In: School review, Vol. 21, 1913, S. 254 – 259)
- Theisen Manuel: Wissenschaftliches Arbeiten — Technik – Methodik – Form. 6. Auflage, München: Verlag Franz Vahlen, 1992
- Tiedemann Joachim: Leistungsversagen in der Schule. 1. Auflage, München / Basel: Ernst Reinhardt Verlag, 1978 (Studienreihe Pädagogische Psychologie)
- Ullrich Heiner & Wöbcke Manfred: Notenelend in der Grundschule — Alternative Beurteilungsformen für die Praxis. München: Kösel-Verlag, 1981
- Viebahn Peter: Schülerselbstbeurteilung in der Leistungsdiagnostik. In: Unterrichtswissenschaft, Heft 1, 1982 (10. Jahrgang), S. 59 – 72
- Vogel Friedrich: Beschreibende und schließende Statistik — Formeln, Definitionen, Erläuterungen, Stichwörter und Tabellen. 9. Auflage, München: Oldenbourg Verlag, 1996
- Wandl Joseph: Der schwache Schüler in der homogen beziehungsweise heterogen zusammengesetzten Klasse — Untersuchungen zu den Auswirkungen homogen beziehungsweise heterogen zusammengesetzter Klassen auf den schwachen Schüler. 1. Auflage, Passau: Andreas-Haller-Verlag, 1987
- Weidig Ernst-Raimund: Die Bewertung von Schülerleistungen. Weinheim: Verlag Julius Beltz, 1961 (Reihe: Studien zur Berufspädagogik, Heft 6)
- Weiner Bernard: Die subjektiven Ursachen von Erfolg und Mißerfolg: Anwendung der Attribuierungstheorie auf das Leistungsverhalten in der Schule. Übersetzt von Axel Brandt. In: Edelstein Wolfgang & Hopf Diether (Hrsg.): Bedingungen des Bildungsprozesses — Psychologische und pädagogische Forschungen zum Lehren und Lernen in der Schule. Stuttgart: Ernst Klett Verlag, 1973, S. 79 – 93
- Weiss Rudolf: Leistungsbeurteilung in den Schulen – Notwendigkeit oder Übel? — Problemanalysen und Verbesserungsvorschläge. Wien / München: Jugend und Volk Verlag, 1989 a
- Weiss Rudolf: Die Zuverlässigkeit der Ziffernbenotung bei Aufsätzen und Rechenarbeiten. In: Ingenkamp Karlheinz (Hrsg.): Die Fragwürdigkeit der Zensurengebung — Texte und Untersuchungsberichte. 8. Auflage, Weinheim / Basel: Beltz Verlag, 1989 b, S. 104 – 116 (Aus: Weiss Rudolf: Zensur und Zeugnis. Linz: Haslinger Verlag, 1965, S. 148 – 159)
- Winter Felix: Schüler lernen Selbstbewertung — Ein Weg zur Veränderung der Leistungsbeurteilung und des Lernens. Frankfurt: Verlag Peter Lang, 1991 (Reihe: Europäische Hochschulschriften: Reihe XI — Pädagogik, Band 480)
- Wittoch Margarita: Unterricht mit Schulversagern — Vorschläge zur Förderung von Lernprozessen. Köln: Verlag Kiepenheuer & Witsch, 1976
- Ziegenspeck Jörg: Zensur und Zeugnis in der Schule — Darstellung der allgemeinen Problematik und der gegenwärtigen Tendenzen. Hannover: Hermann Schroedel Verlag, 1973
- Ziegenspeck Jörg: Zensur und Zeugnis. In: Klauer Karl (Hrsg.): Handbuch der Pädagogischen Diagnostik — Band 3. 1. Auflage, Düsseldorf: Pädagogischer Verlag Schwann, 1978, S. 621 – 632
Fußnoten
- Gemeint sind technische Fachschulen. >zurück in den Text
- Gemeint ist eine Verständigung gemäß § 19 Abs. 4 SchUG (mit 30. Dezember 1996 wurde diese Bestimmung allerdings novelliert), vulgo „Gefährdung“. >zurück in den Text
- Nach der Verständigung, daß ein „Nicht genügend“ droht, hat der Schüler noch mehrere Möglichkeiten, die Berechtigung zum Aufsteigen zu erhalten: eine mündliche Prüfung am Jahresende, einen Beschluß der Klassenkonferenz gemäß § 25 Abs. 2 lit. c SchUG über das Aufsteigen mit einem „Nicht genügend“ (vulgo „Klausel“, seit 1974 möglich) und eine Wiederholungsprüfung zu Beginn des folgenden Schuljahres. >zurück in den Text
- Gemeint sind die im Zuge der Schullaufbahn erworbenen aufeinander aufbauenden Kenntnisse und Fertigkeiten (vgl. Tiedemann, 1978, S. 17). >zurück in den Text
- Quelle: Jugend-Info der Stadt Wien – Wiener Jugendkreis / MA 13 – Landesjugendreferat. >zurück in den Text
- Siehe Anhang 1 (Seite 139). >zurück in den Text
- Der „Missing“-Wert ist jener Wert, der eingegeben wird, wenn bei der betreffenden Frage keine Angabe gemacht wurde. >zurück in den Text
- Feichtinger macht leider keine genaue Angabe über die Anzahl der Befragten. >zurück in den Text
- BGBl. Nr. 767/1996 vom 30. Dezember 1996, mit 1. Feber 1997 in Kraft getreten. § 19 Abs. 4: „Wenn die Leistungen des Schülers auf Grund der bisher erbrachten Leistungen in einem Pflichtgegenstand im zweiten Semester mit ‘Nicht genügend’ zu beurteilen wären, ist dies den Erziehungsberechtigten unverzüglich mitzuteilen und dem Schüler sowie den Erziehungsberechtigten vom Klassenvorstand oder vom unterrichtenden Lehrer Gelegenheit zu einem beratenden Gespräch zu geben. Dabei sind insbesondere leistungsfördernde Maßnahmen zur Vermeidung dieser negativen Beurteilung (zB Analyse der Lerndefizite, Fördermöglichkeiten, Leistungsnachweise, individuelles Förderprofil) zu beraten und ist ein individuelles Förderkonzept zu erarbeiten. Dies gilt für Berufsschulen mit der Maßgabe, daß die Verständigung auch an den Lehrberechtigten zu ergehen hat und an lehrgangsmäßigen Berufsschulen an die Stelle des zweiten Semesters die zweite Hälfte des Lehrganges tritt; diese Verständigungspflicht besteht nicht an lehrgangsmäßigen Berufsschulen mit einer geringeren Dauer als acht Wochen.“ >zurück in den Text