
Überblick über die griechische Mathematik
Seminararbeit
am Institut für Philosophie an der Universität Wien
April 1997
Inhaltsverzeichnis
- Die Mathematik vor den Griechen
- Die Anfänge der Mathematik bei den Griechen
- Pythagoras: Mathematik als Wissenschaft
- Platon und Aristoteles
- Euklid: axiomatische Mathematik
- Archimedes:
Zerstört mir meine Kreise nicht!
- Resümee
- Fußnoten
- Literaturverzeichnis
Die Mathematik vor den Griechen
Aus dieser Zeit (ab ca. 3000 v. Chr.) sind aus unserem Kulturkreis hauptsächlich Aufzeichnungen der Babylonier und Ägypter überliefert, bezüglich letzterer ist vor allem der Papyrus Rhind und der Moskauer Papyrus bedeutsam.
Von den Babyloniern stammt folgendes Beispiel. Es zeigt, daß der Lehrsatz des Pythagoras bereits lange vor dessen Wirken bekannt war:
Eine Stange der Länge 30 (steht an einer Wand). Das obere Ende rutscht um eine Länge von 6 herab. Wie weit bewegt sich das untere Ende der Stange? Quadriere 30, das ergibt 900. Subtrahiere 6 von 30, (das ergibt 24). Quadriere 24, das ergibt 576. Subtrahiere 576 von 900, das ergibt 324. Welche Zahl quadriert ergibt 324? Es ist 18 zum Quadrat. Sie hat sich 18 entlang des Bodens bewegt.(Faber, zitiert nach Schmidt, 1992, S. 3)
Es ist zu beachten, daß der Stab zuerst genau senkrecht an der Wand stand, die Skizze zeigt die Situation nach dem Verrutschen:
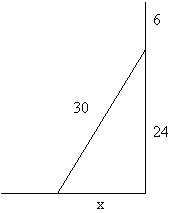
Durch Anwendung des Satzes von Pythagoras erhält man:
30² = 24² + x² und daraus x² = 30² – 24² = 324 also schließlich x = 18.
Aus Ägypten ist folgendes Beispiel überliefert:
Methode zur Berechnung eines Pyramidenstumpfes.(Faber, zitiert nach Schmidt, 1992, S. 6).
Falls es ein Pyramidenstumpf sei, von 6 Kubit Höhe,
Von 4 Kubit an der Basis, und 2 an der Spitze,
Rechne so mit diesen 4, quadriere. Ergebnis 16.
Verdopple 4. Ergebnis 8.
Rechne so mit dieser 2, quadriere. Ergebnis 4.
Zähle diese 16 mit dieser 8 und mit dieser 4 zusammen. Ergebnis 28.
Berechne 1/3 von 6. Ergebnis 2.
Berechne indem du 28 zweimal nimmst. Ergebnis 56.
Hurra! Es ist 56! Du hast das Richtige gefunden.
Diese Methode zur Berechnung des Volumens eines Pyramidenstumpfes stellt die aus heutiger Sicht größte mathematische Leistung der Ägypter dar. Die Herleitung der Formel zeigt, wie komplex der Lösungsweg eigentlich ist. Die Pyramide im Schrägriß:
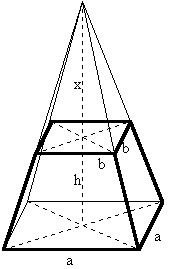
Die allgemeine Formel für das Volumen der Pyramide ist ![]() . Die Berechnung des Volumens des Stumpfes erfolgt, indem vom Volumen der großen Pyramide (Höhe x + h) das der kleinen (Höhe x) abgezogen wird. x ist jedoch unbekannt und muß erst berechnet werden. Dazu betrachten wir die Pyramide im Aufriß:
. Die Berechnung des Volumens des Stumpfes erfolgt, indem vom Volumen der großen Pyramide (Höhe x + h) das der kleinen (Höhe x) abgezogen wird. x ist jedoch unbekannt und muß erst berechnet werden. Dazu betrachten wir die Pyramide im Aufriß:
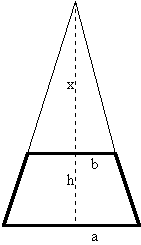
Durch Anwendung des Strahlensatzes gilt aufgrund ähnlicher Dreiecke:
![]()
![]()
ax = bx + bh
ax – bx = bh
x(a – b) = bh
![]()
Das Volumen des Pyramidenstumpfes beträgt daher:
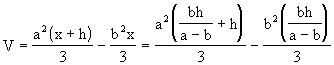
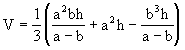
![]()
![]()
![]()
![]()
Durch Polynomdivision erhält man: (a³ – b³) : (a – b) = a² + ab + b². Daher gilt schließlich:
![]()
Das ist die Formel, die oben im Text angewandt wurde.
Diese beiden Beispiele zeigen, daß die Mathematik bereits vor den Griechen weiter entwickelt war, als man vielleicht vermuten würde. Insbesondere die Babylonier waren schon weit fortgeschritten; sie berechneten Gleichungen mit zwei und mehr Unbekannten sowie quadratische Gleichungen, vereinzelt auch Gleichungen höheren Grades.
Aus den obigen Beispielen lassen sich wesentliche Charakteristika der vorgriechischen Mathematik erkennen: Die typischen Fragestellungen kommen aus Problemen des täglichen Lebens, beispielsweise der Nahrungsverteilung oder der Landvermessung. Es wird nur mit konkreten Zahlen gerechnet, man strebt nicht nach Allgemeingültigkeit. Es wird jedes Beispiel individuell gelöst, man sucht nicht nach Gemeinsamkeiten und allgemeinen Lösungen für ähnliche Probleme. Es gibt keine Definitionen, keine Sätze und schon gar keine Beweise.
Die Anfänge der Mathematik bei den Griechen
Der Kaufmann Thales von Milet (erste Hälfte des 6. Jahrhunderts v. Chr.) gilt als wichtigster Vorläufer der wissenschaftlichen Mathematik. Er begann als erster, die Mathematik nicht nur als eine Art Sammlung von Kochrezepten, sondern als eine systematisch geordnete Wissenschaft zu betreiben, wenngleich er dieses Konzept noch nicht vollständig umsetzte. Es ist kein Zufall, daß jener Thales auch als der erste Philosoph gesehen wird, vielmehr zeigt es, daß sich die Griechen im Unterschied zu den Babyloniern und Ägyptern nicht mehr aus hauptsächlich praktischem, sondern aus philosophischem Interesse mit Mathematik beschäftigten.
Die wesentliche Neuerung gegenüber allen anderen vor ihm ist, daß Thales erstmals Voraussetzungen und Sätze formulierte, vor allem aber, daß er auch nach Beweisen für seine Behauptungen suchte. Dabei ließ er sich jedoch nach wie vor von der Anschauung leiten, weshalb er lediglich als Vorläufer der mathematischen Wissenschaft gilt.
In seiner Jugend unternahm Thales Reisen nach Babylon und Ägypten, wo er sich das Wissen dieser Völker aneignete. Auf die Frage, wie hoch er die Cheops-Pyramide schätze, soll er geantwortet haben, daß er sie nicht schätzen, sondern messen werde, und zwar so: Er legte sich in den Sand, um seine Körpergröße am Boden zu markieren. Dann stellte er sich an das Fußende des Abdrucks und wartete, bis sein Schatten genau so lang war, wie der Abdruck. Dann mußte nämlich auch die Pyramide genau so hoch sein, wie ihr Schatten lang, und den konnte man ja leicht messen. Falls man die Messung jedoch zu einer anderen Tageszeit vornehmen wollte, brauchte man nur einen Stab in den Sand zu stecken, und das Verhältnis der Stablänge zur Schattenlänge berechnen. Dasselbe Verhältnis müsse auch für die Pyramide gelten.
Dieser Methode liegt der Strahlensatz zugrunde:
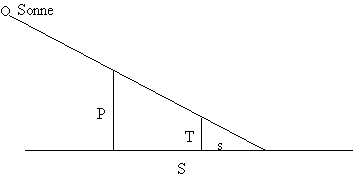
Nun gilt: P : S = T : s, dabei steht P für die Höhe der Pyramide, S für den Schatten der Pyramide, T für Thales und s für den Schatten des Thales.
Tatsächlich ist Thales wahrscheinlich nicht genau so gestanden, daß (im entscheidenden Moment) sein Schatten und jener der Pyramide an der selben Stelle endete (wie es in der Skizze der Fall ist). Aufgrund der großen Entfernung zur Sonne spielt das aber keine Rolle.
Außerdem sind folgende Sätze von Thales überliefert:
- Der Durchmesser halbiert den Kreis.
- Die Basiswinkel im gleichschenkeligen Dreieck sind gleich groß.
- Ein Dreieck ist durch Angabe von zwei Winkeln und einer Seitenlänge eindeutig gegeben. („WWS-Satz“)
- Scheitelwinkel sind gleich groß.
- Jeder Winkel im Halbkreis ist ein rechter. („Satz von Thales“)
Pythagoras: Mathematik als Wissenschaft
Endgültig zur Wissenschaft wurde die Mathematik durch Pythagoras von Samos (zweite Hälfte des 6. Jahrhunderts v. Chr.), einem Schüler des Thales. Ebenso wie dieser soll er zahlreiche Reisen unternommen haben, sicher ist eine nach Ägypten, wo er angeblich in den Kreis der Priester aufgenommen wurde und sich dadurch deren Geheimwissen aneignen konnte.
Später ließ er sich im griechisch besiedelten Kroton (Unteritalien) nieder, wo er eine Art mystische Sekte oder Geheimbund gründete, die auch politisch zu großem Einfluß gelangte. Im Mittelpunkt des Interesses der Mitglieder stand jedoch die Mathematik, die in vier Teilbereiche (sogenannte Mathemata) unterteilt wurde: Arithmetik, Geometrie, Astronomie und Musik (Harmonielehre). Die Römer faßten diese Gebiete unter dem Namen Quadrivium zusammen, das gemeinsam mit dem Trivium (Grammatik, Rhetorik und Dialektik) die sogenannten septem artes liberales bildete. Diese Einteilung wirkte bis in die Neuzeit in Form der Artistenfakultäten an den Universitäten fort.
Was unterscheidet nun aber die „wissenschaftliche“ Mathematik des Pythagoras von jener der alten Babylonier oder Ägypter?
Eudemos von Rhodos, ein Schüler des Aristoteles, schrieb: Nach diesen1 verwandelte Pythagoras die Beschäftigung mit diesem Wissenszweige (Mathematik) in eine wirkliche Wissenschaft, indem er die Grundlage derselben von höherem Gesichtspunkte aus betrachtete und die Theoreme derselben immaterieller und intellektueller erforschte. Er ist es auch, der die Theorie des Irrationalen und die Konstruktion der kosmischen Körper erfand.
(Colerus, 1944, S. 21).
Die große Errungenschaft des Pythagoras war einerseits das Streben nach Allgemeingültigkeit und andererseits das Suchen nach Begründungen (Beweisen). Seine Vorgangsweise war die der Deduktion, die seither ein essentieller Bestandteil der Mathematik ist. So besagt der berühmte, nach ihm benannte, Lehrsatz, daß in jedem rechtwinkeligen Dreieck das Quadrat über der Hypotenuse gleich der Summe der Kathetenquadrate ist. Also auch im speziellen Dreieck mit den Seiten 3, 4 und 5, das schon die Ägypter zur Konstruktion eines rechten Winkels verwendeten, ohne sich jedoch Gedanken darüber zu machen, ob in jedem rechtwinkeligen Dreieck die Seitenlängen ein gewisses Verhältnis haben müssen.
Von dieser Erkenntnis ausgehend begann Pythagoras die Suche nach weiteren Tripel (a,b,c), für die die Beziehung c² = a² + b² gilt. Für ungerade a fand er selbst eine Formel zur Erzeugung solcher sogenannter pythagoräischer Zahlentripel: Für a = 2n + 1 wähle man b = 2n² + 2n und c = 2n² + 2n + 1. Für gerade a wurde eine entsprechende Formel erst von Platon angegeben.
Eigentümlich für die griechische Mathematik waren sogenannte Flächenanlegungen, d. h. gewisse Figuren durch geschicktes „Anlegen“ in andere flächengleiche Figuren zu verwandeln. Dabei wurden sowohl die Strecken als auch die Flächen als Zahlen interpretiert, sodaß mit dieser Methode auch arithmetische Probleme gelöst werden konnten; daher wurde sie später geometrische Algebra genannt.
Ein typisches Beispiel: Wenn sich n als Produkt von a und b darstellen läßt, dann kann n folgendermaßen durch d dividiert werden:
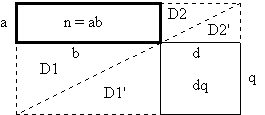
Da offensichtlich die Dreiecke D1 und D1' sowie D2 und D2' gleich groß sind, müssen auch die Rechtecke ab und dq gleich groß sein (das große Rechteck wird durch die Diagonale ja halbiert). Aus ab = dq folgt nun ![]() , d. h. also
, d. h. also ![]() .
.
Die Präferenz für geometrische Lösungen zeigt sich auch im Grundsatz, daß geometrische Fragestellungen stets durch geometrische Methoden zu beantworten sind; als Hilfsmittel sind dabei nur Zirkel und Lineal zugelassen. So auch bei den „drei klassischen Problemen der antiken Mathematik“:
- Winkeldreiteilung: Einen gegebenen Winkel in drei gleiche Winkel teilen.
- Würfelverdoppelung (Deli’sches Problem): Zu einem gegebenen Würfel einen Würfel mit doppeltem Volumen finden.
- Quadratur des Kreises: Zu einem gegebenen Kreis ein flächengleiches Quadrat finden.
Die drei Probleme wurden zwar im Lauf der Zeit (noch lange vor Christi Geburt) gelöst, allerdings nicht durch Konstruktionen mit Zirkel und Lineal. Später wurde gezeigt, daß keine dieser Fragen solcherart lösbar ist.
Doch zurück zu den Pythagoräern: Ihr besonderes Interesse galt den philosophischen Aspekten der Mathematik, dies zeigt sich an ihrer ausgeprägten Zahlenmystik. Für Pythagoras waren Zahlen keine „Erfindungen“ des Menschen, sondern die Essenz aller Dinge. So beruhen nicht nur musikalische Harmonien auf Zahlenproportionen, sondern überhaupt die ganze Welt, der ganze Kosmos ist Harmonie und Zahl.
Durch genaue Untersuchung der Zahlen glaubte man daher, dem Wesen der Dinge auf der Spur zu sein und die ordnenden Prinzipien des Kosmos erkennen zu können. Zu diesem Zwecke wurden die Zahlen nach mehreren Kategorien unterteilt. Die Eins allerdings wurde nicht als Zahl angesehen, sondern als der Ursprung aller Zahlen und damit letztlich als der Ursprung der Welt.
Primzahlen: Eine Zahl ist eine Primzahl, wenn sie außer 1 keine echten Teiler besitzt. Alle anderen Zahlen heißen zusammengesetzte Zahlen.
Gerade Zahlen: Durch 2 teilbare Zahlen heißen gerade, alle anderen heißen ungerade.
Vollkommene Zahlen: Die Summe der Teiler ist das Wesen einer Zahl, dementsprechend ist eine Zahl vollkommen, wenn die Summe ihrer echten Teiler (inklusive 1) die Zahl selbst ergibt. Die kleinste vollkommene Zahl ist 6 (=1 + 2 + 3). Zahlen, deren Teilersumme größer als sie selbst ist, heißen überschießende bzw. übervollkommene, jene, bei denen sie kleiner ist, mangelhafte bzw. untervollkommene Zahlen.
Befreundete Zahlen: Zwei Zahlen heißen befreundet, wenn die Teilersumme der einen die andere ergibt. Bis heute sind nur wenige Paare bekannt, das kleinste ist 220 und 284 (220 = 1 + 2 + 4 + 71 + 142 und 284 = 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110).
Darauf aufbauend wurden den Zahlen gewisse Eigenschaften zugesprochen, z. B. beschränkt – unbeschränkt, rechts – links, männlich – weiblich, Ruhe – Bewegung, gekrümmt – ungekrümmt, gut – böse. So galten beispielsweise gerade Zahlen als weiblich und ungerade als männlich. 5 war als Summe der kleinsten weiblichen und der kleinsten männlichen (2 + 3) die Zahl der Ehe.
Außerdem gab es noch sogenannte figurierte Zahlen, das waren durch kleine Steinchen aufgelegte Figuren. Die Zahlen wurden nach der entstehenden Figur benannt:
Dreieckszahlen:
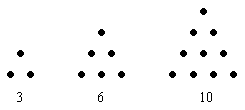
Quadratzahlen:
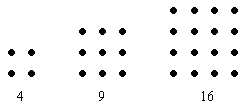
Fünfeckszahlen:
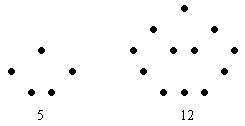
Jene Steinchen, die von der einen auf die nächste Zahl dazukommen, hießen Gnomon, hier sind das die weißen Steinchen:
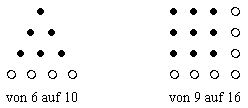
Durch Untersuchung dieser Gnomone erhielt man eine Reihe von elementaren Resultaten, beispielsweise, daß die Summe der ersten n Zahlen eine Dreieckszahl ist, daß die Summe der ersten n ungeraden Zahlen eine Quadratzahl ist, usw. Auch kompliziertere Probleme, wie z. B. die Summe der ersten n Quadratzahlen, wurden von den Pythagoräern so gelöst. Für die Mathematik waren das die ersten Anfänge der Zahlentheorie, sowie der Beschäftigung mit Folgen und Reihen.
Da die Eins für die Pythagoräer als Ursprung der Welt unteilbar war, waren Brüche nicht zulässig, statt dessen verwendeten sie Proportionen. Dies erklärt auch die etwas eigenartige Nähe zur Musik, da sich die Höhe eines Tones in Abhängigkeit von der Länge der gestrichenen Saite verändert. Daher betrachteten sie die Lehre von der Harmonie letztlich als eine Lehre von Zahlenverhältnissen. Je nach Art des Verhältnisses wurde zwischen arithmetischer, geometrischer und harmonischer Proportion unterschieden, diese Namen tragen auch heute noch die entsprechenden Mittelwerte.
In der Musik waren alle auftretenden Proportionen ganzzahlig, sodaß die Pythagoräer zu der Ansicht gelangten, daß alles, was in der Welt harmonisch ist, durch ganzzahlige Verhältnisse ausgedrückt werden kann. Umso schwerer wurden sie von der Entdeckung irrationaler Verhältnisse getroffen, noch dazu dort, wo sie es am wenigsten erwartet hatten: In einem Quadrat (also einer höchst harmonischen, regelmäßigen Figur) läßt sich das Verhältnis der Seiten zur Diagonale nämlich nicht durch ganze Zahlen ausdrücken. Bei Seitenlänge 1 hat die Diagonale ja bekanntlich die Länge ![]() , und diese beiden Größen können nicht durch Multiplikation mit ganzen Zahlen ineinander übergeführt werden, sie sind inkommensurabel.
, und diese beiden Größen können nicht durch Multiplikation mit ganzen Zahlen ineinander übergeführt werden, sie sind inkommensurabel.
Diese Entdeckung versetzte der ganzen pythagoräischen Auffassung von der Welt einen schweren Schlag, da nun offensichtlich nicht mehr alle Zahlen (und damit die ganze Welt) durch Vervielfachung der Einheit Eins entstanden sein kann.
Diese Krise wurde durch die berühmten Paradoxien des Zenon von Elea (erste Hälfte des 5. Jahrhunderts v. Chr.) noch verstärkt. Durch scharfsinnige Beispiele brachte Zenon die Auffassung, jede Strecke (und der gesamte Raum) sei eine Ansammlung von einzelnen Punkten, ins Wanken. Die bekannteste Paradoxie ist jene von Achilles und der Schildkröte, hier in Versform inklusive Lösung (Cremer, 1982):
Achilles und die Schildkröte
A. Einleitung
Wieder mal geb ich die Sporen
dem geplagten Pegasus,
knall die Peitsch ihm um die Ohren,
daß er fort mich tragen muß,
dorthin, dorthin, denn ich will es,
wo man keinen Mangoldt kennt,
wo die Kröte mit Achilles
um den Preis Olympias rennt.B. Ausführung
Der Zenon, den ein jeder kennt,
war zu Elea einst Dozent.
Er schrieb gar viel, was schön und wichtig,
es war nur leider niemals richtig.
Die Mathematische Wissenschaft
war ihm noch ziemlich schleierhaft;
jedoch, als ob er was verstände,
schrieb er darüber ganze Bände.
Als einstens er beim Morgenfraß
mal recht vergnügt im Schlafrock saß
und im Athener Tageblatte
das Wichtigste gelesen hatte
(die marathonische Keilerei,
den Aufruf der „Griechischen Volkspartei“),
sprach schmunzelnd er: „Hm, hm, ja, ja,
jetzt mach’ ma mal so’n Sophisma!Schildkröten sind uns hierzuland
als plump und langsam wohl bekannt.
Achill, so schließ ich, weil ich hell,
läuft sicherlich zehnmal so schnell.
Je nun, er rennt, so denk ich mir,
mal um die Wette mit dem Tier.
Zehn Meter Vorsprung geb’ er bloß;
dies Zugeständnis scheint nicht groß.
Die Glocke tönt, der Kampf fängt an,
nun, gute Kröte, halt’ dich ran!
Zehn Meter läuft Achilles heiter;
die Kröte ist ’nen Meter weiter.
Auch diesen läuft Achill in Eil;
die Kröte läuft den zehnten Teil.
Auch dieses Stück durchmißt Achill,
doch ach, das Vieh steht auch nicht still;
sie ist trotz allem etwas weiter;
Achilles ist schon nicht mehr heiter.
So wiederholt sich stets dies Spiel,
und nimmer kommt der Held zum Ziel.*)*) Der Schluß ist ja impertinent!
Die Reihe ist doch konvergent!Nimmt er der Kröte alten Ort,
schwupp! ist sie auch schon wieder fort.
Er kommt in Wut bis zur Ekstase;
die Kröte dreht ihm eine Nase.
Sie bleibt ihm stets ein Stück voraus;
Achilles schleicht geknickt nach Haus;
die Kröte aber triumphiert
und wird mit Orden dekoriert.“(Oh, Zenon, Zenon, alter Wicht,
kennst Du den Kowalewski nicht?)Als Zenon dies verfertigt hat,
schickt er es gleich dem Tageblatt;
die Redaktion, dieweil sie helle,
zahlt eine Drachme auf der Stelle
und bringt das Zeug nach einer Weile
recht groß im Unterhaltungsteile.
Man liest’s, soweit man gut gelaunt,
man räuspert sich und ist erstaunt,
ist halb erfreut und halb ergrimmt,
doch weiß man nicht, weshalb’s nicht stimmt.Das kam, weil, das ist sonnenklar,
der Mangoldt nicht erfunden war!
Hätt man gehört bei Dr. Feigl,
der Zenon trüg kein Lorbeerzweigl;
man hätt gewußt, was uns verständlich:
Der Wert der Reihe ist ja endlich!
Ihr Limes ist, so schließ ich schlau,
sogar der Treffpunkt ganz genau.
Da in der Reihe, wie wir sehn,
nur positive Glieder stehn,
die Teilsumme, wie Ihr wohl wißt,
stets kleiner als der Limes ist.
Indem er nun nur Stellen zählt,
die vor dem Treffpunkt sind gewählt,
lügt er dem biedern Publiko
nun vor, es bliebe immer so!
Und das besagte Publikum
glaubt ihm das alles, weil es dumm.
Wir glauben’s nicht, denn wir sind schlau;
wir wissen so was ganz genau.C. Schluß
Und die Moral von der Geschicht:
Es geht halt ohne Mangoldt nicht!
So kauf ihn Dir noch heute drum;
sonst kostet’s mehr, und das wär dumm.
Platon und Aristoteles
Platon (erste Hälfte des 4. Jahrhunderts v. Chr.) machte das Quadrivium – und damit die Mathematik – zu einer der Hauptsäulen der Bildung in seiner Akademie. Die Mathematik eignete sich seiner Meinung nach besonders zur Schulung des Geistes für die Philosophie. Die Welt der mathematischen Gegenstände ist nämlich eine Vorstufe zur Welt der Ideen, dementsprechend stellt die Beschäftigung mit der Mathematik gemäß dem Höhlengleichnis einen entscheidenden Schritt von der Welt der Schatten in Richtung der Welt der Ideen – und damit zur höchsten Lehre, der Philosophie – dar. Insofern sind die mathematischen Objekte keine Konstruktionen des menschlichen Geistes, sondern (immaterielle) Gegebenheiten, die von den Menschen erforscht werden.
Besondere Bedeutung hatten für Platon die seit den Pythagoräern bekannten
fünf regelmäßigen Polyeder. Diese Körper seien gerade
die Formen, aus denen die Welt aufgebaut ist: die Atome des Feuers seien Tetraeder2,
die der Luft Oktaeder3,
die des Wassers Ikosaeder4
und die der Erde Würfel. Der ganze Kosmos habe schließlich die Gestalt des Pentagondodekaeders5,
welcher der vollkommenste Polyeder sei, weil er der Kugel am ähnlichsten sei.
(Bajlicz, 1993, S. 29).
Aristoteles (4. Jahrhundert v. Chr.) legte durch die Gründung seiner auf Axiomen aufbauenden Logik den Grundstein für die weitere Entwicklung der Mathematik als deduktive Wissenschaft, die auf (möglichst wenigen) Axiomen aufbaut. Im Rahmen der Syllogistik untermauerte er die damals vorherrschende Beweismethode der Zurückführung des Gegenteils auf einen Widerspruch (indirekter Beweis), indem er Regeln für die Umkehrung einer Aussage angab.
Euklid: axiomatische Mathematik
Euklid (4. bis 3. Jahrhundert v. Chr.) verfaßte das bedeutendste mathematische Buch aller Zeiten, die „Elemente“. Er legte damit den Grundstein für die axiomatische Mathematik im heutigen Sinn, indem er zuerst Axiome formulierte, aus denen er dann Sätze ableitete. Sein Werk war so bahnbrechend und ausgereift, daß es bis ins vorige Jahrhundert allgemein anerkannte Gültigkeit besaß und als Unterrichtsgrundlage verwendet wurde. Erst um die Jahrhundertwende gelang eine Ergänzung der Arbeiten Euklids und damit die endgültige Axiomatisierung der Geometrie.
Einige Beispiele für sogenannte Postulate:
(Schmidt, 1992, S. 8)„Das folgende sei möglich:
- Eine Gerade von einem beliebigen Punkt zu einem beliebigen Punkt zu ziehen.
- Eine begrenzte Strecke in eine unbegrenzte Gerade zu verlängern.
- Einen Kreis mit beliebigem Mittelpunkt und Radius zu zeichnen.“
Eine herausragende Stellung nimmt das sogenannte Parallelenaxiom ein, das besagt, daß zu einer Gerade durch einen beliebigen Punkt genau eine parallele Gerade existiere. Jahrhundertelang versuchten Mathematiker, diese Forderung aus den anderen Axiomen herzuleiten, bis man schließlich einsehen mußte, daß dies unmöglich ist. Im Zuge dieser Versuche entdeckte man jedoch die nicht-euklidische Geometrie, die durch Ersetzung bzw. Weglassung einiger der Euklidschen Axiome entsteht.
Der größte Teil der „Elemente“ befaßt sich mit geometrischen Problemen, allerdings teilweise mit solchen, die heute der Algebra zugerechnet werden. Da damals noch keine algebraische Symbolik existierte, mußten jedoch sämtliche Aussagen geometrisch formuliert werden, wie beispielsweise: Das Quadrat über der Summe von zwei Strecken ist flächengleich mit der Summe der beiden Quadratflächen plus der zweifachen Rechtecksfläche aus diesen beiden Strecken.
(Mößlacher, 1993, S. 42), was nichts anderes bedeutet als (a + b)² = a² + b² + 2ab.
In der Geometrie bewies er unter anderem, daß außer den bereits bekanntenfünf regelmäßigen Polyedern keine weiteren existieren; in der Zahlentheorie, daß es unendlich viele Primzahlen gibt; und als Vorläufer der Infinitesimalrechnung löste er die erste Maximumsaufgabe, indem er zeigte, daß jenes Rechteck, daß bei gegebenen Umfang einen maximalen Flächeninhalt hat, ein Quadrat ist. Außerdem erfand er den nach ihm benannten euklidischen Algorithmus zur Berechnung des größten gemeinsamen Teilers zweier Zahlen.
Archimedes: Zerstört mir meine Kreise nicht!
Archimedes (3. Jahrhundert v. Chr.) gilt als der größte Mathematiker der Antike. Aus heutiger Sicht ist vor allem seine Beschäftigung mit krummlinig begrenzten Figuren und Körpern (Kreis, Kugel, Zylinder, Parabel, Ellipse, Paraboloid, Ellipsoid, Hyperboloid etc.) bahnbrechend: So berechnete er beispielsweise den Flächeninhalt des Parabelsegments, indem er es durch immer kleiner werdende Dreiecke solange approximierte, bis die Differenz zwischen der Parabelfläche und der Fläche der Dreiecke kleiner als jedes gewünschte Maß war. Da er dadurch die Parabel gleichsam mit Dreiecken von innen heraus „ausschöpfte“ nannte man dieses Verfahren später Exhaustionsmethode; dies war der Beginn der Integralrechnung.
Auf ähnliche Weise fand er Formeln für die Oberfläche und das Volumen der Kugel und eine erste Annäherung an pi.
Aus philosophischer Sicht brach Archimedes mit der Tradition der eleatischen Lehre des Parmenides, nämlich der Auffassung aller geometrischen Objekte als ruhendes, ewiges Sein. Dieser Standpunkt hatte in den Ideen des Platon und der Geometrie des Euklid seinen Höhepunkt erfahren. War ein Kreis für Euklid die Gesamtheit oder der Inbegriff aller Punkte, für die der Abstand von einem bevorzugten Punkt (dem sogenannten Mittelpunkt) gleich ist
(Colerus, 1944, S. 62), so ist er für Archimedes das Ergebnis einer Zirkelbewegung. Dementsprechend erklärt er die nach ihm benannte archimedische Spirale als die Bewegung eines Punktes (von innen nach außen) auf einem sich gleichförmig (um seinen Ursprung) drehenden Strahl.
Einzigartig war auch seine für die Griechen unübliche Beschäftigung mit großen Zahlen, und zwar in der Größenordnung bis 1063 (das ist eine Zahl mit 63 Nullen), für die er eine eigene Notation erfand. Darüber hinaus erklärte er, daß sich die natürlichen Zahlen bis ins Unendliche fortsetzen lassen. In diese Kerbe schlägt auch das archimedische Axiom, das besagt, daß sich durch Vervielfachung einer gegebenen Strecke jede beliebige noch so lange Strecke übertreffen lasse.
An die Wurzeln der griechischen Mathematik bei den Babyloniern und Ägyptern erinnert Archimedes’ ausgeprägter Sinn für die Praxis: Anders als Euklid leitete er seine Erkenntnisse nicht von vorn herein aus den Axiomen ab, sondern gewann sie teilweise aus mechanischen Beobachtungen. Diese verallgemeinerte er, und bewies sie erst danach. Diese Mischung aus Induktion und Deduktion ist in gewissen Bereichen bis heute die gängige Methode der mathematischen Forschung.
Aber auch am anderen Ende seines Erkenntnisprozesses bedachte Archimedes die Praxis, wenn es nämlich darum ging, sein gefundenes Wissen anzuwenden. So wird berichtet, daß sich seine Heimatstadt Syrakus nur deshalb so lange vor der Eroberung durch die Römer wehren konnte, weil Archimedes neuartige Kampfmaschinen entworfen hatte.
Im Jahre 212 v. Chr. fiel Syrakus schließlich. Römische Legionäre trafen Archimedes als Greis in seinem Garten sitzend an, als er Skizzen in den Sand zeichnete. Er soll sie nur mit den Worten Zerstört mir meine Kreise nicht!
bedacht haben, sie aber erschlugen ihn, und so wurde der letzte große griechische Mathematiker ein Opfer der neuen aufstrebenden Macht im Mittelmeerraum. Diese Wendung des Schicksals hat beinahe symbolischen Charakter, denn was die Entwicklung der Mathematik betrifft, folgen Jahrhunderte der Stagnation, in denen die Haupttätigkeit im Kopieren, Kommentieren und Bewahren lag.
Resümee
Die Griechen waren es, die die Mathematik von einer reinen Technik zu einer Wissenschaft erhoben, und diese sukzessive erweiterten, vertieften und bezüglich ihrer Grundlagen festigten. Ihre große Neuerung lag zweifellos darin, daß sie mit einer vollkommen anderen Einstellung an dieses Wissensgebiet herangingen, als die Völker vor ihnen. Erinnern wir uns an den Text der Babylonier (Quadriere 30, das ergibt 900. Subtrahiere 6 von 30, (das ergibt 24). Quadriere 24, das ergibt 576.
) und vergleichen ihn mit einem der ersten Erkenntnisse der Griechen: Der Durchmesser halbiert den Kreis.
Ein Kontrast, wie er stärker kaum sein könnte!
Der Stellenwert des Rechnens zeigt sich schon auf den ersten Blick bei Betrachtung der Notation von Zahlen: Während sowohl die Babylonier als auch die Ägypter über relativ ausgeklügelte Zahlensysteme verfügten, benützten die Griechen ihr Alphabet: Die ersten neun Buchstaben bezeichneten 1 bis 9, die nächsten neun die Zehnereinheiten von 10 bis 90, und dann wieder neun für die Hunderter von 100 bis 900; da das Alphabet mit 24 Buchstaben dafür nicht mehr ausreichte, wurden kurzerhand drei neue „Buchstaben“ eingeführt. Wie „handlich“ dieses System für Rechnungen ist, kann man sich leicht vorstellen, es gibt nämlich keine Ziffern mit Stellenwert, sondern jede Zahl muß als ganzes betrachtet werden. Wenn dann noch zufällig die Buchstabenfolge einer Zahl ein sinnvolles Wort ergab, war die Verwirrung perfekt.
Dieser Mangel erklärt auch die Entstehung der „geometrischen Algebra“ und das strikte Verhaften bei der Geometrie, auch bei Problemen, die heute der Algebra zugerechnet werden. Eine solche konnte sich bei den Griechen nicht entwickeln, da keine entsprechende Symbolik verfügbar war. Diese entstand erst später, beginnend mit Diophant von Alexandria (3. Jahrhundert n. Chr.).
Fußnoten
Gemeint sind Thales von Milet und ein gewisser Mamerkos, von dem wir nur den Namen kennen.
(Colerus, 1944, S. 21 Fußnote). >zurück in den Text- die von vier gleichseitigen Dreiecken begrenzte gleichseitige dreieckige Pyramide >zurück in den Text
- der von acht gleichseitigen Dreiecken begrenzte regelmäßige Körper >zurück in den Text
- der von zwanzig gleichseitigen Dreiecken begrenzte regelmäßige Körper >zurück in den Text
- der von zwölf regelmäßigen Fünfecken begrenzte regelmäßige Körper >zurück in den Text
Literaturverzeichnis
- (Ohne Name) (1990): Platon. S. 370 in:
Gottwald Siegfried & Ilgauds Hans-Joachim & Schlote Karl-Heinz [Hrsg.]: Lexikon bedeutender Mathematiker. Leipzig: Bibliographisches Institut - Bajlicz Klaudia (1993): Quadrivium - mathematischer Bildungskanon in Antike und Mittelalter. Diplomarbeit an der Formal- und Naturwissenschaftlichen Fakultät der Universität Wien
- Brentjes Sonja (1990): Archimides. S. 25–26 in:
Gottwald Siegfried & Ilgauds Hans-Joachim & Schlote Karl-Heinz [Hrsg.]: Lexikon bedeutender Mathematiker. Leipzig: Bibliographisches Institut - Brentjes Sonja (1990): Euklid. S. 138–139 in:
Gottwald Siegfried &Ilgauds Hans-Joachim & Schlote Karl-Heinz [Hrsg.]: Lexikon bedeutender Mathematiker. Leipzig: Bibliographisches Institut - Brentjes Sonja (1990): Pythagoras von Samos. S. 382–384 in:
Gottwald Siegfried &Ilgauds Hans-Joachim & Schlote Karl-Heinz (Hrsg.): Lexikon bedeutender Mathematiker. Leipzig: Bibliographisches Institut - Brentjes Sonja (1990): Thales von Milet. S. 456 in:
Gottwald Siegfried &Ilgauds Hans-Joachim & Schlote Karl-Heinz (Hrsg.): Lexikon bedeutender Mathematiker. Leipzig: Bibliographisches Institut - Colerus Egmont (1944): Von Pythagoras bis Hilbert — Die Epochen der Mathematik und ihre Baumeister — Geschichte der Mathematik für jedermann. Berlin / Wien / Leipzig: Karl Bischoff Verlag
- Cremer Hubert (1982): Carmina mathematica. 7. Auflage, Aachen: Verlag J. A. Mayer
- Faber R. (1992): Foundation of Euclidian and Non-Euclidian Geometry. Verlag Marcel Dekker. Zitiert nach Schmidt
- Falkner Claudia (1989): Die Entwicklung der Infinitesimalrechnung von der Antike bis zu Newton und Leibniz. Diplomarbeit an der Formal- und Naturwissenschaftlichen Fakultät der Universität Wien
- Mößlacher Brigitte (1993): Arithmetik und Algebra in Antike und Mittelalter des Abendlandes. Diplomarbeit an der Formal- und Naturwissenschaftlichen Fakultät der Universität Wien
- Schenk Günter (1990): Aristoteles. S. 27–28 in:
Gottwald Siegfried & Ilgauds Hans-Joachim & Schlote Karl-Heinz [Hrsg.]: Lexikon bedeutender Mathematiker. Leipzig: Bibliographisches Institut - Schmidt Andrea (1992): Grundlagen der Geometrie. Diplomarbeit an der Formal- und Naturwissenschaftlichen Fakultät der Universität Wien
- Struik Dirk (1967): A Concise History of Mathematics. 3. Auflage, New York: Dover Publications